P1040023

obliczamy maksymalną niepewność systematyczną wielkości z ze wzoru

n

pt = £

H

fi

Aa:,.

Dla większej liczby wielkości mierzonych bezpośrednio (i > 2) lepsze oszacowanie niepewności maksymalnej uzyskuje się za pomocą wzoru

Az| =

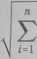
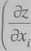
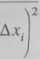
13. SZACOWANIE NIEPEWNOŚCI PRZYPADKOWYCH

Przy pomiarach wielkości fizycznych w sytuacjach, w których podstawową rolę odgrywają niepewności przypadkowe, wszystkie oceny dokładności pomiarów można podać jedynie ^:z pewnym prawdopodobieństwem.

Potencjalnie możemy wykonać nieograniczoną liczbę pomiarów na elementach zbioru utworzonego przez obiekty pomiaru (np. kulki lub wałki danego typu) lub nawet na jednym obiekcie (np. średnice długiego drutu można mierzyć w różnych punktach).

Zjawiska (w tym również pomiary), które można powtarzać nieograniczoną liczbę razy nazywamy zjawiskami masowymi. Badaniem i • ilościowym opisem prawidłowości występujących w* zjawiskach masowych zajmuje się statystyka matematyczna.

W szczególności statystyka matematyczna dostarcza metod wnioskowania

0    wartości parametrów opisujących całą populację na podstawie Wyników uzyskanych dla losowo wybranej części zbioru (zwanej próbą). Wynik poszczególnego pomiaru wchodzącego w skład tego zbioru jest zdarzeniem losowym.

Przyczyn powodujących niepewności przypadkowe może być wiele. Przykładowo, rozrzut średnicy nakrętek produkowanych przez automat może być powodowany przez: niejednorodność materiału, wahania temperatury, zużycie narzędzi, drgania itp. Każda z nich wnosi swój wkład w rozrzut średnicy

1    wkłady te sumują się.

Z centralnego twierdzenia granicznego rachunku prawdopodobieństwa wynika, że rozkład sumy zmiennych losowych jest zbliżony do rozkładu normalnego, stąd rozkład normalny zmiennej losowej ma tak wielkie znaczenie praktyczne Odchylenie standardowe i wariancja tego rozkładu są podstawowymi parametrami, które wykorzystuje się jako miarę niepewności przypadkowych wyników pomiarów.

Postępowanie przy szacowaniu niepewności przypadkowych jest następujące:

1. Jako oszacowanie niewiadomej wartości wielkości mierzonej należy przyjąć wartość średniej arytmetycznej z próby

n

Wartość średnia x z serii n pomiarów jest również (podobnie jak wynik pojedynczego pomiaru x) zmienną losową;

2. Jako oszacowanie: odchylenia standardowego a w populacji przyjmujemy wartość jf określoną za pomoc«pvzcfu '

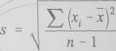
3. Odchylenie standardowe średniej arytmetycznej obliczamy z zależności

^Sx g

Y _ p/_x\    *-

4. Z rozkładu t -Studenta t = -— będącego aproksymacją względnego

odchylenia średniej z próbki x od średniej dla populacji generalnej E(pc) możemy określić niepewność przypadkową określenia wartości średniej:

Wartość m dobieramy z tablic statystycznych po przyjęciu wartości dwu parametrów (a i /), od których zależy wartość krytyczna t_a ,. Parametr f = n - 1 jest liczbą stopni swobody, a parametr a jest poziomem istotności. Zakładając prawdopodobieństwo P (ufność), z jakim chcemy wyznaczyć granice przedziału A* (obejmującego prawdziwą wartość wyniku pomiaru), możemy poziom istotności a Otrzymać ze związku a = 1 -P.

Pytania kontrolne

1.    Podać różnice między pomiarem bezpośrednim a pośrednim.

2.    Omówić pojęcia: błąd pomiaru i niepewność pomiaru.

3.    Omówić główne przyczyny:

—    błędów nadmiernych (grubych),

—    błędów systematycznych,

—    niepewności przypadkowych,

—    niepewności systematycznych.

11