P3040941

4J Wytoczenie elementów ściskanych

Jeśli założymy, że ugięcie 8 na rys.4.2b jest małe, możemy przyjąć, że 5*61/3, czyli:

(4.3)

PS = />2^{6 = 2/f0}’

a stąd:

(4.4)

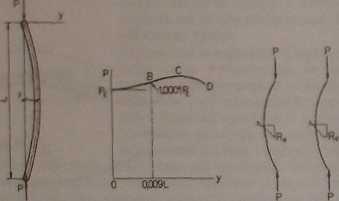
Otrzymano więc wzór na wartość krytycznego obciążenia P, ale brak poza tym informacji o ugięciu 5, które będzie niewyznaczalne, jeśli problem będzie rozwiązany w sposób wyżej opisany. To rozwiązanie problemu stateczności sprężystej jest opisane przez zbiór punktów OA i EAD na rys.4.2c, z którego wynika, że 5 jest zero dla dowolnej wartości P mniejszej od obciążenia krytycznego, ale może mieć pewne małe wartości (obejmujące również zero) przy obciążeniu krytycznym. W tym sensie mogą być dwie postacie równowagi elementu przy krytycznym obciążeniu, a mianowicie jedna postać opisuje element jako prosty, a druga jako nieznacznie ugięty. Krytyczne obciążenie odpowiada więc bifurka-cyjnym postaciom równowagi.

b)

c) d)

•)

Ry**4.3. Odkształceniu i naprężenia pręta osiowo ściskanego

Na ry8.4.3a pokazano pierwotnie prosty, jednorodny, przegubowo umocowany i osiowo obciążony element, który wyboczył się. Element ten stanowić może model słupa. W dowolnym punkcie ugiętej jego osi moment zginąjący jest równy P y. Z warunków równowagi wynika związek:

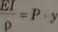
(4.6)

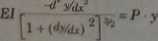
Stosując znane wyrażenie na krzywiznę 1/p , otrzyma się: 2 «

(4.6)

Równanie (4.6) jest nieliniowe ze względu na geometrię i można je rozwiązać, stosując całki eliptyczne (61) lub funkcje Bessela (64).

Celem wyznaczenia obciążenia krytycznego zakłada się, że ugięcia są małe; można napisać wtedy:

(4.7)

Podstawy projektowania konstrukcji metalowych

Podstawiając

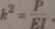
(44)

otrzyma się:

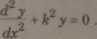
(44)

W wyniku rozwiązania tego równania z uwzględnieniem warunków brzegowych słupa jak na rys.4.3a otrzyma się wzór na:

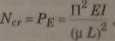
(4.10)

gdzie:

Pg — obciążenie krytyczne w sensie Eulera,

|i — współczynnik zależny od sposobu zamocowania końców elementu ściskanego.

Ponieważ formuła (4.10) jest ważna tylko wówczas, jeśli naprężenie w elemencie ściskanym nie przekracza wartości granicy proporcjonalności, związek (4.10) można zapisać następująco:

_o =^f>B_ss n²Ei _m n²E ^B A A (pL)² " (p/d)² '

(4.11)

gdzie:

A — pole przekroju poprzecznego,

i — promień bezwładności przekroju poprzecznego elementu ściskanego,

p — współczynnik zależny od sposobu zamocowania końców tego elementu.

Przyjmując Ó za ugięcie w środku długości elementu, to rozwiązanie równania (4.9) opisywać będzie kształt osi ugiętej przy obciążeniu Eulera:

(4.12)

Postać krzywej osi ugiętej me będzie jednak jednoznacznie określona, gdyż równanie (4.12) jest rozwiązaniem przybliżonym równanie (4.6). Sens fizyczny tego problemu jest podobny do rozwiązania zagadnienia ściskanego pręta ze sprężyną (rys.4.2a). Jeśli więc zamiast wartości

p

współrzędnej <rys.4.2c) podstawi się współrzędną P/Pg. to krzywa

CAB będzie wtedy opisywać charakterystykę pręta osiowo ściskanego siłą P równą i wyższą sile krytycznej Pg (rys.4.3b).

Przybliżone rozwiązanie zagadnienia stateczności elementu ściskanego z końcami zamocowanymi przegubowo można napisać w postaci (32):

Dokładność wartości P z rozwiązania (4.13) jest rzędu 19 przy wartościach SIL do 0,25.

Na rys.4.2c krzywa CAB opisiąje również równanie (4.13) w układzie współrzędnych P/Pg, SIL.

Dla S/L = 0,1 wartość P/Pg obliczona z równania (4.13) równa jest 1,0123. Jeśli element ściskany o wysokości 3 m będzie obciążony siłą P = 1,0123 Pg, to jego ugięcie będzie równe 0,3 m przy założeniu, żs