P3200286

152

Zatem otrzymujemy u + v = [14,10,4] = 2 -[7,5,2] u-v= [-2,2,2] = 2 - [-1,1,1].

Odp.: Proste będące szukanymi dwusiecznymi kątów mają równania

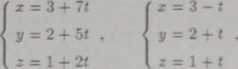
gdzie t £ R.

r Jeżeli chcemy wiedzieć, które z równań odpowiadają dwusiecznej kąta ostrego, to należy zbadać znak wyrażenia u o u. Mamy u o v = 48 + 24 + 3 > 0, zatem kąt między wektorami u, r jest ostry, więc wektor uĄ- v wyznacza dwusieczną kąta ostrego.

Gil. Wyznaczyć równania parametryczne prostej będącej rzutem prostopadłym prostej Jp |s    na płaszczyznę

4® + y + z — 3 = 0 oraz wyznaczyć kąt, jaki tworzy dana prosta z daną płaszczyzną.

1° Wyznaczymy kąt między prostą li a daną płaszczyzną, więc najpierw zbadamy wzajemne położenie prostej i płaszczyzny.

N

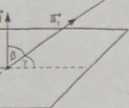
Dla li mamy di = [2,2, —1], Pi(0,5,— 1).

Dla płaszczyzny mamy N = [4,1,1]. Prosta będzie równoległa do płaszczyzny, gdy oi -L N.

OioiV = 8 + 2- l = 9jź0

Stąd prosta nie jest równoległa do płaszczyzny, więc prosta przecina płaszczyznę.

(Prosta nie jest prostopadła do płaszczyzny, gdyż di ^ N.)

dl o Ń = |di| - \Ń\ • cos fi — y/4 + m ■ V16 + 1 + 1 - cos fi =

= 3 • 3VI - cos fi = 9\/2 cos fi Zatem otrzymujemy, że 9>/2cos fi = 9.

2    4    4

2

Odp.; Dana prosta tworzy z daną płaszczyzną kąt }.

2° Wyznaczymy rzut prostopadły prostej na płaszczyznę.

* = -1 -1

Stąd mamy 8t + 5 + 2t-l-t-3 = 0, czyli 9t = -1, więc t = 2

Wystarczy znaleźć punkt przecięcia się prostej z płaszczyzną oraz znaleźć rzut dowolnego punktu prostej l\ (np. punktu Pi (0,5,—1)) na płaszczyznę, następnie napisać równanie prostej przechodzącej przez te dwa znalezione punkty.    _ t

9

2    43

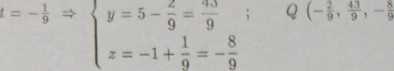
• Znajdziemy rzut prostopadły punktu Pi(0,5,-1) na płaszczyznę 4® + y + *- 3 = 0.

Wyznaczamy prostą, która prze

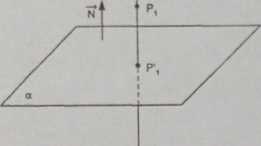
chodzi przez P\ i jest prostopadła do płaszczyzny, więc jej wektorem kierunkowym może

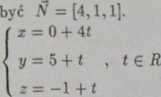
Punkt P[ jest punktem wspólnym wyznaczonej prostej i danej płaszczyzny.