P1111278

60 VIII. Funkcja pierwotna (całka nieoznaczona)

przekształca całkę następująco:

64

3375

/ (2-/*)*<*

teraz można albo powtórzyć w wypadku szczególnym ogólne rachunki z 284, III (a), albo skorzystać z go. towego wzoru (12).

Odpowiedź:

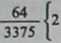
4x-l

<2x*-x+2)»'*

1.    (4x-l)»    1    (4x-l)^ł    1,

6 (2x²-x+2)³'²    160 (2x²—x+2)^5/2 J    *

4) f    (x+3)dx

^J (x*-x+l)/x²+x+l

Podstawienie

x

/+!

daje

. . ... .    (M²±H+l)t²+l2/ir±(ji+v)+2]t+(v²+v+\)

^{± +}    (t+iy

Warunki 2pt+(p+t)+2 = 0 lub ju-ł-v = 0, pv = —1 będą spełnione na przykład dla fi = 1, v =» —1. Mamy

r—1    . _    2dt

7+r*    (f+i)*’

x+3 =

4/+2

x²— x+l

r² + 3 (/+!)*

i/x²+x+i =

jeśli przyjąć dla ustalenia uwagi, ie r+1 >0, tzn. x<l. Tak więc

f (x+3)dx    r    (8/+4) dt

' (x^a-x+l)yGF+x+T J (r²+3) V^r3f^a+1

Otrzymana całka równa się sumie całek

+1

f-*^==+4 f-—

^J (r^ł+3)i/3r²+i ^J (r²+3)|/37^T

Pierwszą całkę można, jak widać, łatwo obliczyć za pomocą podstawienia u = ]/3t²+l i równa się ona V8arc ^t8'|/-—g⁺~- + C*. Do drugiej zastosujemy podstawienie Abela

.3/

l/3?MT

które sprowadza ją do postaci

f * - ^1 lnl	3 l/T +2l/2u
27—8a^a ^^ln	3 ]/3" —2^2«

+c-

Pozostaje tylko powrócić do zmiennej x.

s) rc^+pyWs+i -x»+i _rfT

^    ^X?+X+l—X

Wskazówka: Przedstawić funkcję podcałkową w postaci

2x*+x³-t-2x^a+l

x+l

1    2x⁵+2x*+3x*-l

(x+l)Vx*+x+l

=: (2x*-x²+3x-3)+ —-

x+l

2x*+3x²—3x+3 ₁_4

V^rxⁱ+x+l    (x+l) yx²+x+l

do trzeciego składnika zastosować metodę z ustępu 284,1, do ostatniego zaś — podstawienie x+1 =* 1/r

§ 4. Całkowanie wyrażeń zawierających funkcje trygonometryczne i funkcję wykładniczą

286. Całkowanie różniczek R (sin x, cos x) dx. Różniczki tego typu można zawsze

sprowadzić do postaci wymiernej podstawieniem t = tg -2-x(—« < x < 7t). Rzeczywiście,

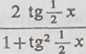
sin x =

cos x =

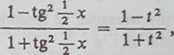
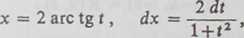
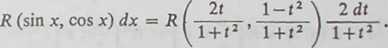
Tak więc całki typu

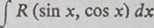
mogą być zawsze obliczone w postaci skończonej. Wyrażają się one przez funkcje, które spotykamy przy całkowaniu różniczek wymiernych oraz przez funkcje trygonometryczne.

Wspomniane podstawienie uniwersalne dla całek typu (1) prowadzi niekiedy do skomplikowanych rachunków. Podamy dalej przypadki, gdy cel ten można osiągnąć za pomocą prostszych podstawień. Najpierw zrobimy następującą elementarną uwagę z dziedziny algebry.

Jeśli funkcja wymierna całkowita lub ułamkowa R(u,v) nie zmienia swej wartości przy zmianie znaku jednego z argumentów, na przykład w, tzn. jeśli

R(-u_tv) « R(u,v)_t

to można ją sprowadzić do postaci zawierającej tylko parzyste potęgi u.