PC043359

Botdiiat J. Funkcje Jednej zmiennej

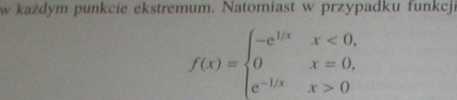
mamy /'(O) — f'(0) = ...** O, jednak w punkcie x = O funkcja ta nie ^ ekstremum. Wyznaczanie największej i najmniejszej wartości funkcji iia dziale (a. b) znacznie się upraszcza, gdy funkcja jest różniczkowalna na (a,b Wewnątrz przedziału najmniejsza wartość funkcji i największa wartość funt cji mogą być osiągane jedynie w tych punktach, w których pochodna funta jest równa 0. Należy jeszcze zbadać funkcję w otoczeniach punktów końcowM przedziału. Często wystarczy w tym celu wyznaczyć granice lim f(x), lim fU\ oraz wartości f(a), f(b) (p. rys. 3.4)

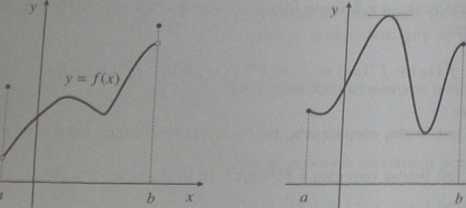
b x

y-fa)

Rys. 3.4. Jeśli funkcja jest różniczkowalna, to wartości największą i najmniejszą (o De istnieją) osiąga na końcach przedziałów lub wśród tych punktów, w których pochodna lej

funkcji jest równa 0

Źródło: opracowanie własne

Przykład 3.45.

Wyznaczymy największą i najmniejszą wartość funkcji f(x) = x² - •£, * € (1,2).

Funkcja jest ciągła na przedziale (1,2) i różniczkowalna wewnątrz tego przedziału, przy czym pochodna f'{x) = 2x + -4 jest tam dodatnia. Dla końców przedziału mamy /(1) = 0,/(2) = l. Wartości te stanowią, odpowiednio, najmniejszą i największą wartość funkcji na wskazanym przedziale.

Definicja 3.18.

Funkcję f nazywamy wypukłą na przedziale / wtedy i tylko wtedy, gdy dla dowolnych liczb a,f3 > 0, dla których a +0 = 1, jest spełniony warunek

(3.17)

/\ f{ax\ +J3x₂) < af(x 1) +0f(x₂).

Jeśli w (3.17) równość zachodzi Jedynie w przypadku, gdy a * 0, a ■ I lub jti = X2, to mówimy, że funkcja / jest ściśle wypukła.

Mówimy, że f jest wklęsła (ściśle wklęsła) na / wtedy I tylko wtedy, gdy funkcja —f jest wypukła (ściśle wypukła).

Uwaga. Funkcja / jest wypukła (wklęsła) na / = (a. b), a < b, jeśli odcinek łączący dwa punkty wykresu tej funkcji nie jest położony niżej (wyżej) od części wykresu tej funkcji ograniczonej punktami o odciętych x = a oraz x - b (rys. 3.5).

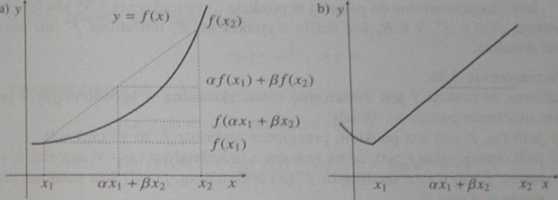
Rys. 3.5. Wykres funkcji ściśle wypukłej (a) i wypukłej (b) Źródło: opracowanie własne

Dla funkcji różniczkowalnych mamy następującą charakterystykę funkcji wypukłych i wklęsłych:

Twierdzenie 3.34.

Załóżmy, że funkcja f jest różniczkowalna w sposób ciągły na przedziale (a,b).

a)    Funkcja f jest wypukła na (a, b) wtedy i tylko wtedy, gdy pochodna /' jest niemalejąca na tym przedziale.

b)    Funkcja / jest wypukła na (a, b) wtedy i tylko wtedy, gdy dla wszystkich x,xo 6 (a,b) zachodzi nierówność

f(x) > /(*o) + f\xo)(x - Xq).

Przykład 3.46.

Z faktu, że funkcja sin x jest wklęsła na przedziale (0, §> wynikają na przykład nierówności £x < sin x x.

Z wklęsłości funkcji ln;r wynika, że In* < x - I dla x > 0.

Z wypukłości funkcji e* wynika, że dla wszystkich x e R mamy e* > x + i.

Definicja 3.19.

Punkt (xo,f(xo)) nazywamy punktem przegięcia wykresu funkcji / wtedy i tylko wtedy, gdy istnieje takie r > 0, że w jednym z przedziałów (xo~r,xo), (x₀,xq + r) funkcja jest wypukła, a w drugim wklęsła.

129