44694 PC043349

Rdzdziat 3. Funkcje jednej zmiennej

Podstawiając w twierdzeniu 3.9 jc = -1, otrzymujemy wynik pntyfcjw

Przykład 3.12.

Wybaczymy granicę ciągu

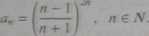
Przekształcając podane wyrażenie, otrzymujemy

On

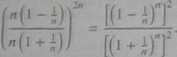
Korzystając z twierdzeń 3.2 i 3.9, łatwo zauważyć, że licznik dąży do e"³,

- do e², rozważany ciąg zaś do er*.

Przykład 3.13.

wynosić

Ciągi postaci (1 + |)", n e N, pojawiają się w wielu zagadnieniach ekonoma tylko), na przykład przy okazji rozważań nad ciągłym oprocentowaniem loka pm nycfi: Przedstawimy pokrótce to zagadnienie. Przypuśćmy, że dysponujemy pewaw pieniędzy kg, którą chcemy wpłacić na rachunek w banku na okres 1 roku. jest oprocentowany ze stałą roczną stopą procentową x, odsetki zaś są dopisy^ kapitału n-krotnie w ciągu roku w stałych odstępach czasu (zatem co i roku), sywana sytuacja odpowiada /i-krotnej kapitalizacji wkładu w ciągu roku. PoągjJ. pierwszego okresu - początkowa kwota ko zostanie powiększona o należne za ten&-odsetki w wysokości k&c-j; tak, że stan konta wyniesie kg +■ koX ■ £ = k^\ +ł). Kt> ta będzie podlegać (procentowaniu w kolejnym okresie, na końcu którego stula będzie wynosić kg (l +    = fc₀ (l + fjj - Po kolejnych okresach stan konta tyi

przy czym ostatnia wartość jest stanem konta po roku. Ciągłą kapitalizację wkłada* żerny sobie wyobrazić jako przypadek, w którym odsetki są dopisywane „bez ppij - nieskończenie wiele razy i nieskończenie często, co odpowiada przejściu granem n -* oo (liczba kapitalizacji rośnie nieograniczenie), a równoważnie |    0 (tfe

okresu pomiędzy sąsiednimi kapitalizacjami wkładu maleje do 0). Otrzymujemf iii graniczną wartość stanu konta równą

Definicja 3.6.

Niech (a„) będzie dowolnym ciągiem liczb rzeczywistych, (m„) zaś rosnąc)¹ ciągiem liczb naturalnych. Ciąg (b„) taki, że dla każdego n € N, b, =«* nazywamy podciągiem ciągu (a_n).

3.1. Ciągi liczbowe

Przykład 3.14.

Rozważmy ciąg (a„), gdzie a„ - (-1)". W przypadku podciągu złożonego z wyrazów

0    numerach parzystych mamy m„ = 1n, gdzie nu N. zatem podciąg jest okrcMntiy przez

b_m.-OŻA— (—    = 1. Dla podciągu o wyrazach nieparzystych mamy m„ = 2n - 1

1    w konsekwencji b_m„ - a^i — (-l)²""’ =—l.

Twierdzenie 3.10.

Gąg ma granicę g wtedy i tylko wtedy, gdy każdy podciąg tego ciągu ma granicę g.

Z ostatniego twierdzenia wynika w szczególności, że pominięcie skończonej liczby wyrazów ciągu nie wpływa na istnienie i wartość granicy ciągu.

Jeśli w danym, ciągu istnieją podciągi mające różne granice, to ciąg ten nie ma granicy. Zatem w przykładzie 3.4 uzyskaliśmy poprawny wynik, ale stosując znacznie trudniejszą wersję postępowania w porównaniu do tej, którą oferuje nam twierdzenie 3.10.

Przykład 3.15.

Gąg a;, =■ (-1)" nie ma granicy.

Istotnie, podciągi złożone z wyrazów o numerach parzystych i nieparzystych są zbieżne, odpowiednio, do liczb 1 i —1. Istnieją zatem podciągi zbieżne do różnych granic.

Definicja 3.7.

i Dla danego ciągu (a„) symbolem

limsupon (odpowiednio liminf a*)

/l—*oo    fl-»oo

oznaczamy największą (odpowiednio najmniejszą) spośród granic podciągów tego ciągu i nazywamy ją granicą górną (odpowiednio granicą dolną.) tego ciągu.

Przykład 3.16.

aj Mamy lim sup(-T)" = 1 oraz lim inf(—!)" = —t. b) lim sup = lim inf = 0.

Dla każdego ciągu istnieją granice dolna r górna, a ponadto jest spełniony warunek lim inf a„ < lim sup a„. Ciąg (a§f ma granicę a wtedy i tylko wtedy,

#*—♦00    rt—*00

gdy lim inf a„ = lim sup On - a.

n-*oo    <»

Dla granic tych można sformułować twierdzenia analogiczne do poprzednich twierdzeń. Przykładowo dla dowolnych ciągów (a„), (b„) zachodzą związki: lim sup(a„ + b„) < lim sup a„ + lim sup b*,

ił—*oo    rt—*co    it—*oa

lim sup(ora„) = ar lim supa„ dla ar > O, lim sup(atfn) = a lim inf a„ dla a < 0.

n—*oo    n—*oo

109