skanuj0118

234

Wówczas torem ruchu jest elipsa opisana równaniem:

(1)

x² y² 2xy    . ,

T + TT—r^cos^=^sm a    b    ab

której osie symetrii na ogół nie pokrywają się z kierunkami drgań składowych

»..y-

Rozważmy przypadki szczególne:

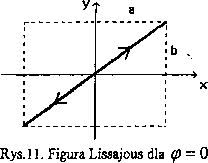
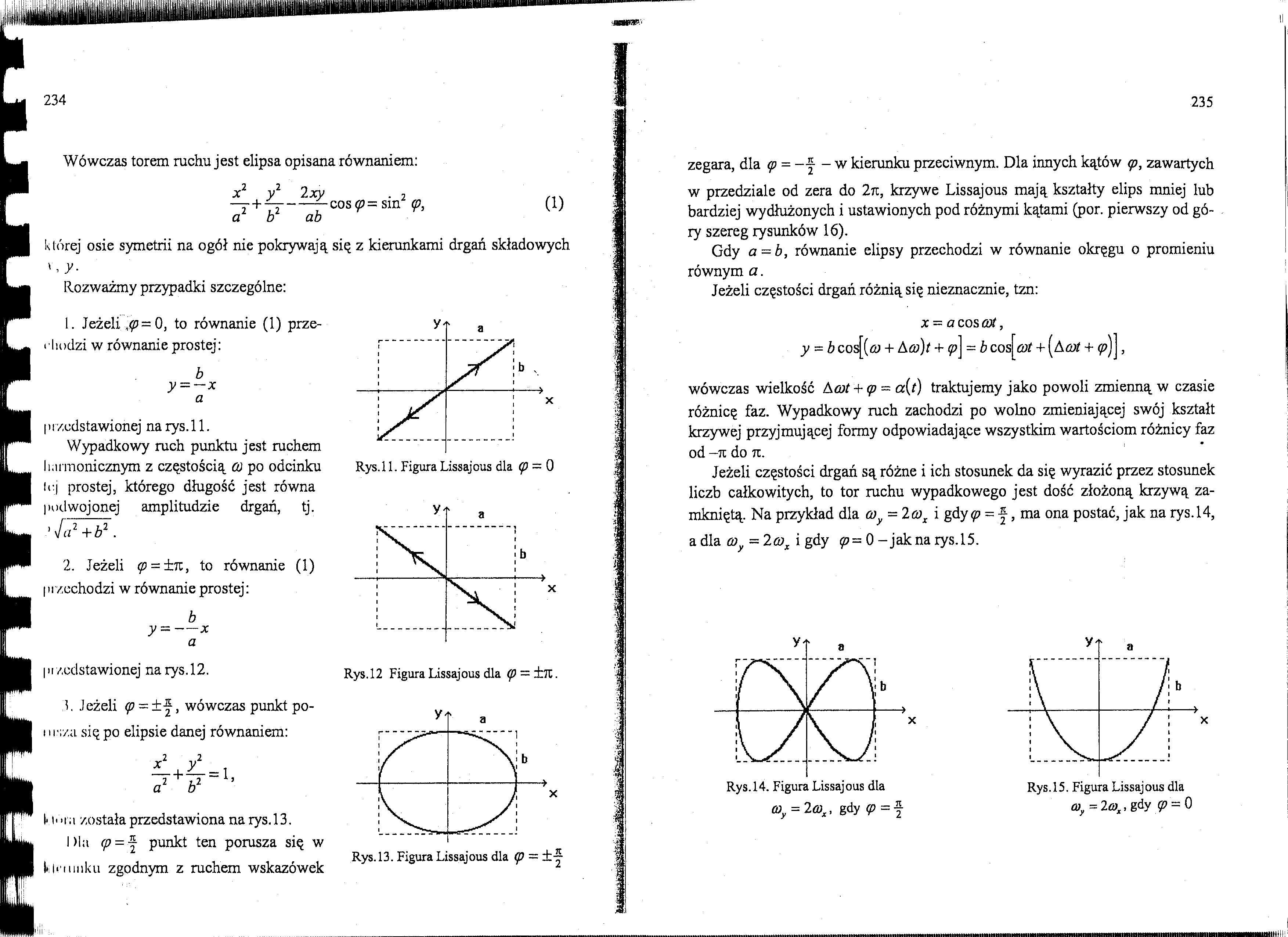
1.    Jeżeli ;tp=Q, to równanie (1) prze-rhodzi w równanie prostej:

b

y = -x a

przedstawionej narys.ll.

Wypadkowy ruch punktu jest ruchem li.irmonicznym z częstością co po odcinku lej prostej, którego długość jest równa podwojonej amplitudzie drgań, tj.

'ja²+b².

2.    Jeżeli ę = +n, to równanie (1) przechodzi w równanie prostej:

b

y = —x a

I    u /odstawionej na rys. 12.

1. Jeżeli ę-±^, wówczas punkt po-

II    r;/;i się po elipsie danej równaniem:

- + ^- = 1 a b

|< i. >ra została przedstawiona na rys.13.

Dla q> = f punkt ten porusza się w Mn miku zgodnym z ruchem wskazówek

zegara, dla ę = -y - w kierunku przeciwnym. Dla innych kątów ę, zawartych

w przedziale od zera do 2n, krzywe Lissajous mają kształty elips mniej lub bardziej wydłużonych i ustawionych pod różnymi kątami (por. pierwszy od góry szereg rysunków 16).

Gdy a-b, równanie elipsy przechodzi w równanie okręgu o promieniu równym a.

Jeżeli częstości drgań różnią się nieznacznie, tzn:

x = a cos cot,

wówczas wielkość Aa>t + ę = a(t) traktujemy jako powoli zmienną w czasie różnicę faz. Wypadkowy ruch zachodzi po wolno zmieniającej swój kształt krzywej przyjmującej formy odpowiadające wszystkim wartościom różnicy faz od -k do 7i.

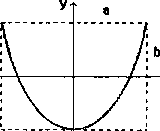
Jeżeli częstości drgań są różne i ich stosunek da się wyrazić przez stosunek liczb całkowitych, to tor ruchu wypadkowego jest dość złożoną krzywą zamkniętą. Na przykład dla o)_y-2co_x i gdy<p = y, ma ona postać, jak na rys. 14, a dla co_y = 2co_x i gdy <p= 0 -jak na rys.15.

y

a

x

Rys. 14. Figura Lissajous dla 0)_y = 2 eo_z, gdy ę =

x

Rys. 15. Figura Lissajous dla a_y = 2a_x, gdy ę? = 0

2