str056

1

metody /.iiwnnmkowuncj / niewiadomymi do rów miń |in|nnu>l. metody pośrcd nicząccj, pozostawiając po prostu poprawkę V_pK / jednc| simiiy /miku równości, u pozostała część równania przenosząc na druga. W len '.posóli otrzymamy

■(A Ul

|M/

l»K

^A»,.k)

™ T577r^dM"⁺ d^/t ^dH«⁺

^V,.K -    +    +    AH_pk) (3.36)

P    P    P

co sprowadza zagadnienie do metody pośredniczącej.

Jest oczywiste, że zestawione na tej podstawie równania normalne pozwalają obliczyć błędy średnie fundacji niewiadomych w sposób odpowiedni dla metody pośredniczącej. Wykażemy też, że suma kwadratów poprawek obserwacyjnych v, konieczna do obliczenia błędu m_o, może być prosto wyrażona przez poprawki V. Mamy bowiem, z uwagi na równość v_pK = — v_Kp

£vv = Sv² + Ev² = 2£v²

PK ¹ KP    PK

oraz

(3.37)

(3.38)

jest więc skąd

gdzie: r - liczba przęseł zaobserwowanych dwustronnie, s - liczba wyznaczanych punktów sieci.

Postępowanie rachunkowe jest w omawianym przypadku znacznie prostsze niż przytoczony tok rozumowania. Prześledzimy to na przykładzie liczbowym.

Przykład 4

Mając dane z przykładu 1, wyrównać sieć niwelacji trygonometrycznej metodą pośredniączącą, zakładając, że oba kąty każdego przęsła zaobserwowano synchronicznie. Obliczyć błędy średnie wysokości wyrównanych oraz błąd średni różnicy wysokości A = H₂ — H₃, jeśli obserwacje są jednakowo dokładne. Odległości skośne S przyjąć za stałe.

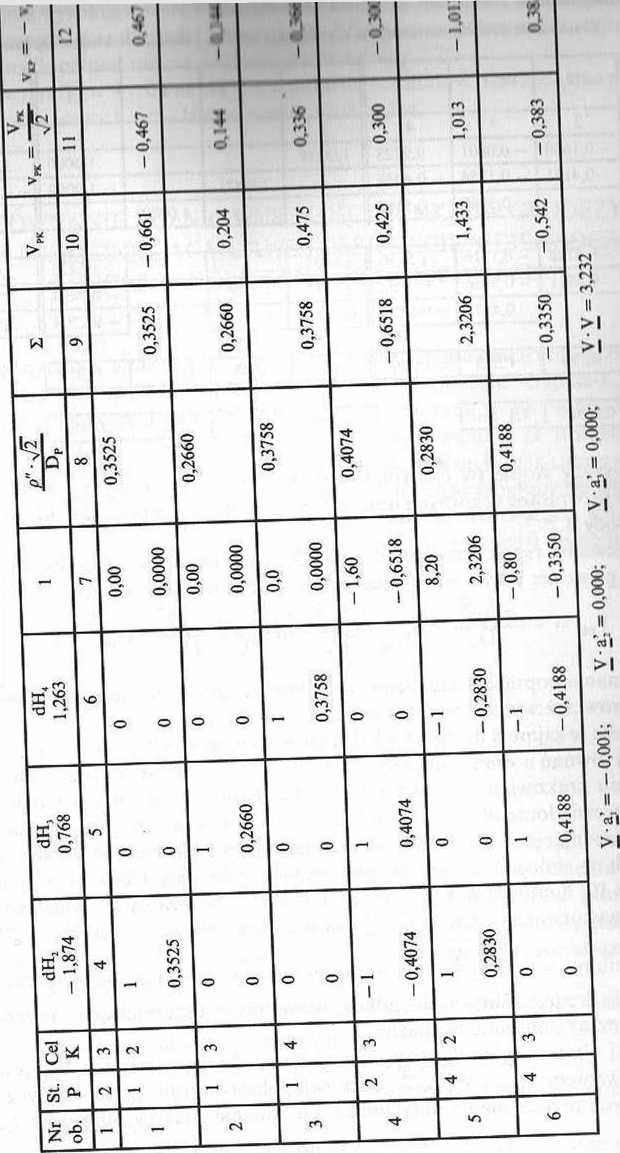
Dane zawiera tablica 3.1, rozwiązanie — tablice 3.29 i 3.30.

Początkowa faza obliczeń jest identyczna z podaną w tablicach 3.21 i 3.22. Jej rezultatem są przybliżone wartości wysokości punktów U^pr/ oraz różnica (o = AH_p^ — AH_pK, wpisane w kolumnie 6 tablicy 3.23, które, jak widać z (3.36), wykorzystamy do rachunku wyrazów wolnych. Dalszy tok pracy ma przebieg następujący.

Dla każdego przęsła zestawiamy jedno równanie poprawki identyczne ze stosowanym przy wyrównaniu niwelacji geometrycznej

v' =-dH +dH + AH^pr/ — AH

PK    P ¹ K    PK    PK

i

Zestawienie równań poprawek

a

o

>1

Kil'⁰

II

S