02

<

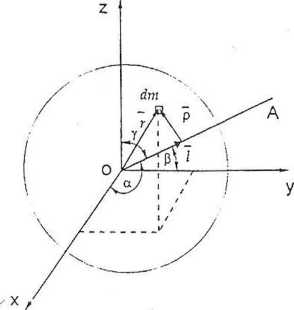
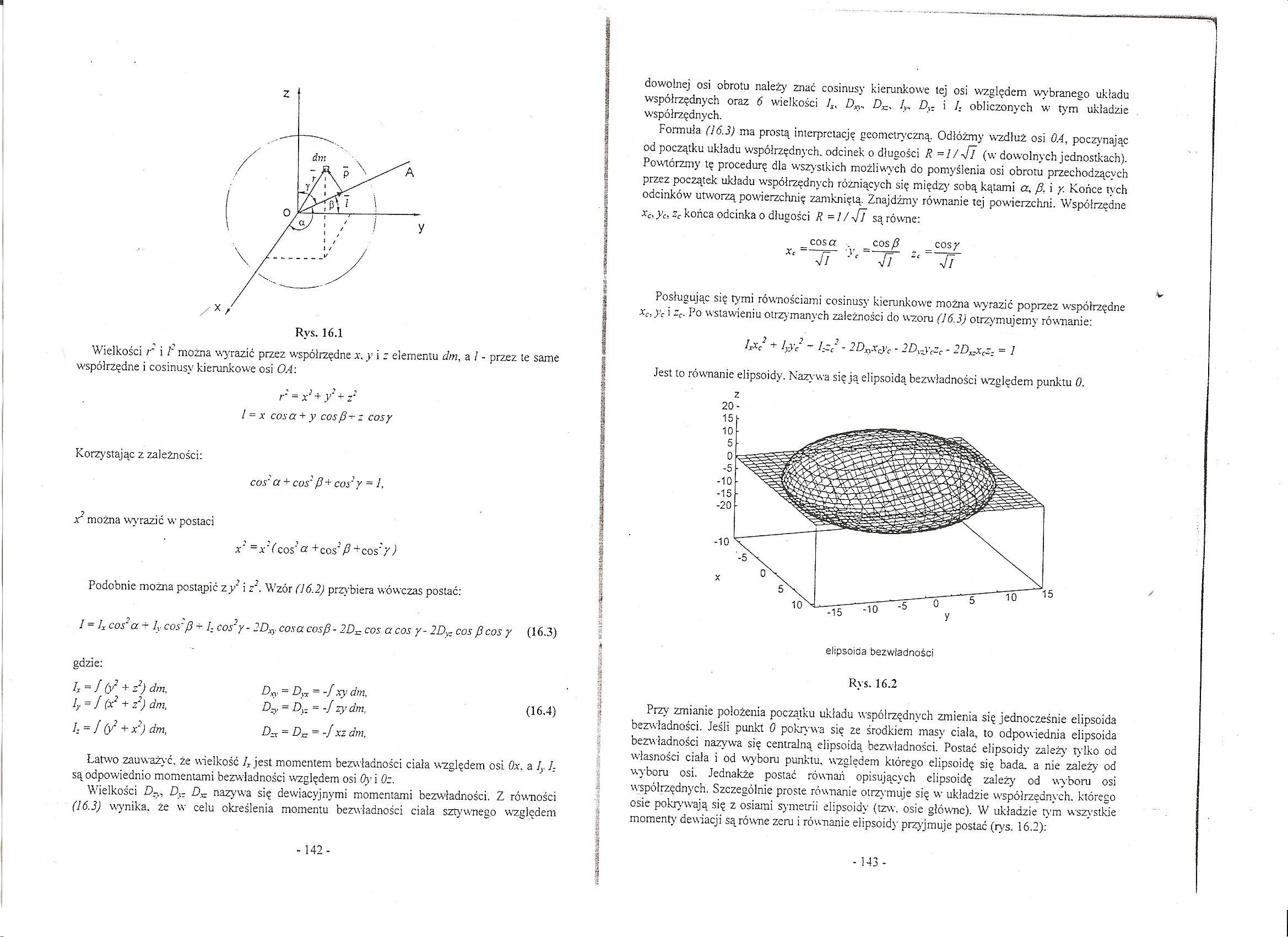
Rys. 16.1

Wielkości i" i /* można wyrazić przez współrzędne x. y i r elementu dm, a / - przez te same współrzędne i cosinusy kierunkowe osi OA:

r = x^; + / + z^;

l = x co.v a + y cos P~ z cosy

Korzystając z zależności:

cos' a + cos² P + cos² y = 1.

x² można wyrazić w postaci

~x'(cos'« +COS²P +COŚ"/)

Podobnie można postąpić zy² i z². Wzór (16.2) przybiera wówczas postać:

I = l_x cos- a - l_y cos' p + I cos²y - 2D_xy cos a cosp - 2D^ cos a cos y- 2D_V- cos p cos y (16.3)

(16.4)

gdzie:

h = / (y² + z²) dm, l_y ~ / (x² + z²) dm,

h~/(y²⁺ x²) dm,

D_xy = D_yx = -f xy dm, Dy = D,_r = -/ zy dm,

D-_x = D_c = -/ xz dm,

Łatwo zauważyć, że wielkość I_x jest momentem bezwładności ciała względem osi 0x, a I_y 1_: są odpowiednio momentami bezwładności względem osi Oy i Oz.

Wielkości D-,, D_r_ Z)._c nazywa się dewiacyjnymi momentami bezwładności. Z równości (16.3) wynika, że w celu określenia momentu bezwładności ciała sztywnego względem

dowolnej osi obrotu należy znać cosinusy kierunkowe tej osi względem wybranego układu współrzędnych oraz 6 wielkości l_x, D^..    7_y, i I_: obliczonych w- t>'m układzie

współrzędnych.

Formuła (16.3) ma prostą interpretację geometryczną. Odłóżmy wzdłuż osi OA, poczynając od początku układu współrzędnych, odcinek o długości R =1 / 41 (w dowolnych jednostkach). Powtórzmy tę procedurę dla wszystkich możliwych do pomyślenia osi obrotu przechodzących przez początek układu współrzędnych różniących się między sobą kątami a, (3, i y. Końce u ch odcinków utworzą powierzchnię zamkniętą. Znajdźmy równanie tej powierzchni. Współrzędne x_Ciy_c, z_c końca odcinka o długości R = 1 / %/7 są równe:

_cosa _cos/7 cosy

^Xc=~7T ^yr~7T ^{Zc =}~7T

Posługując się tymi równościami cosinusy kierunkowe można wyrazić poprzez współrzędne x_c.y_e i z_c. Po wstawieniu otrzymanych zależności do wzoru (16.3) otrzymujemy równanie:

lxXc + ly}'/ - /-- 2D_X)x₍y_c - 2Dy_cz_c - 2D_x:x_cz_z = 1

Jest to równanie elipsoidy. Nazywa się ją elipsoidą bezwładności względem punktu 0.

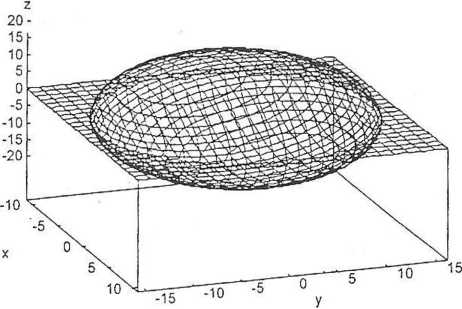
elipsoida bezwładności Rys. 16.2

Przy zmianie położenia początku układu współrzędnych zmienia się jednocześnie elipsoida bezwładności. Jeśli punkt 0 pokrywa się ze środkiem masy ciała, to odpowiednia elipsoida bezwładności nazywa się centralną elipsoidą bezwładności. Postać elipsoidy zależy' tylko od własności ciała i od wyboru punktu, względem którego elipsoidę się bada. a nie zależy od wyboru osi. Jednakże postać równań opisujących elipsoidę zależy' od wyboru osi współrzędnych. Szczególnie proste równanie otrzymuje się w układzie współrzędnych, którego osie pokrywąją się z osiami symetrii elipsoidy (tzw. osie główne). W układzie tym wszystkie momenty’ dewiacji są równe zeru i równanie elipsoidy przyjmuje postać (r\'S. 16.2):

- 143 -