113

Kula równoważna

Jest tylko jedna bryła, którą można opisać jedną liczbą. Jest to oczywiście kula. Jeżeli stwierdzimy, że wymiar (średnica) kuli wynosi 50 p.m, to nie ma żadnych wątpliwości, o jaką kulę chodzi. Używając jednej wartości liczbowej, nie możemy opisać nawet sześcianu, ponieważ wymiar 50 pm może równie dobrze dotyczyć długości krawędzi, jak i długości przekątnej. W przypadku naszego pudełka zapałek, wiele jego cech można opisać jedną liczbą. Na przykład masę, objętość czy pole powierzchni. Tak więc, jeśli potrafimy zmierzyć masę pudełka, to możemy określić wymiar kuli o tej samej masie, czyli tzw. kuli równoważnej. Na tym właśnie polega koncepcja kuli równoważnej. Mierzymy określoną własność badanej cząstki (np. masę, objętość, powierzchnię, maksymalny wymiar), a następnie wyprowadzamy - przy użyciu wzorów na objętość lub powierzchnię kuli - wymiar kuli równoważnej, czyli kuli mającej dokładnie tę samą wartość oznaczanej własności, co rzeczywista cząstka badanego materiału. Ten sposób postępowania umożliwia opisywanie badanych cząstek za pomocą tylko jednego wymiaru. Oczywiście, scharakteryzowanie cząstek trójwymiarowych kilkoma wartościami byłoby bardziej dokładne, ale bez porównania mniej wygodne. Poniżej, (rys. 3.7) przedstawiono prosty przykład ziarna w postaci walca o średnicy podstawy D\ = 20 pm i wysokości h = 100 |im, i odpowiadającą mu pod względem objętości kulę równoważną o średnicy D₂ = 39 pm.

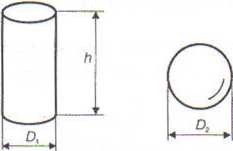
Rys. 3.7. Ziarno w kształcie walca i równoważna mu pod względem objętości kula

Zależność wyników analizy składu ziarnowego od sposobu prowadzenia pomiaru

Kiedy patrzymy na cząstkę pod mikroskopem, to oglądamy jej rzut dwuwymiarowy. Można znaleźć wiele średnic, które będą charakteryzować analizowaną cząstkę. Jeżeli przyjmiemy maksymalną długość za wymiar cząstki, wtedy kulą równoważną dla tej cząstki będzie kula o średnicy odpowiadającej tej długości. Z kolei, jeśli za wymiar cząstki obierzemy minimalną jej długość, to reprezentować ją będzie kula równoważna o średnicy równej tej właśnie długości, a zatem, analizując skład ziarnowy materiału, otrzymamy inny wynik. Dlatego konieczne jest uwzględnienie faktu, że każda metoda pomiarowa, która mierzy inną wielkość cząstki (maksymalną długość, minimalną długość, objętość, pole powierzchni itd.) będzie dawała inny wynik końcowy. Rysunek 3.8 przedstawia różne warianty pomiarów i różne wymiary kul równoważnych dla pojedynczego ziarna piasku.

Najczęściej analizy składu ziarnowego prowadzi się pod kątem określenia udziału frakcji ziarnowych o różnych wymiarach. W ten sposób przedstawia się wyniki prawie wszystkich badań składu granulometrycznego. Jednak w większości metod pomiarowych, opartych na analizie sedymentacyjnej i separacji powietrznej, o zawartości różnych pod względem wymiarów frakcji świadczą zjawiska fizyczne związane bezpośrednio z masą analizowanych cząsteczek. Gdy ziarna badanego materiału charakteryzują się w przybliżeniu stałą gęstością, można przyjąć, że masa cząsteczek jest proporcjonalna do ich objętości, a zatem także do ich

113