35360 Image68 (7)

134

c. Przy zsuwaniu się bez tarcia ruch obrotowy nie występuje. Zgodnie z zasadą zachowania energii (rys.49)

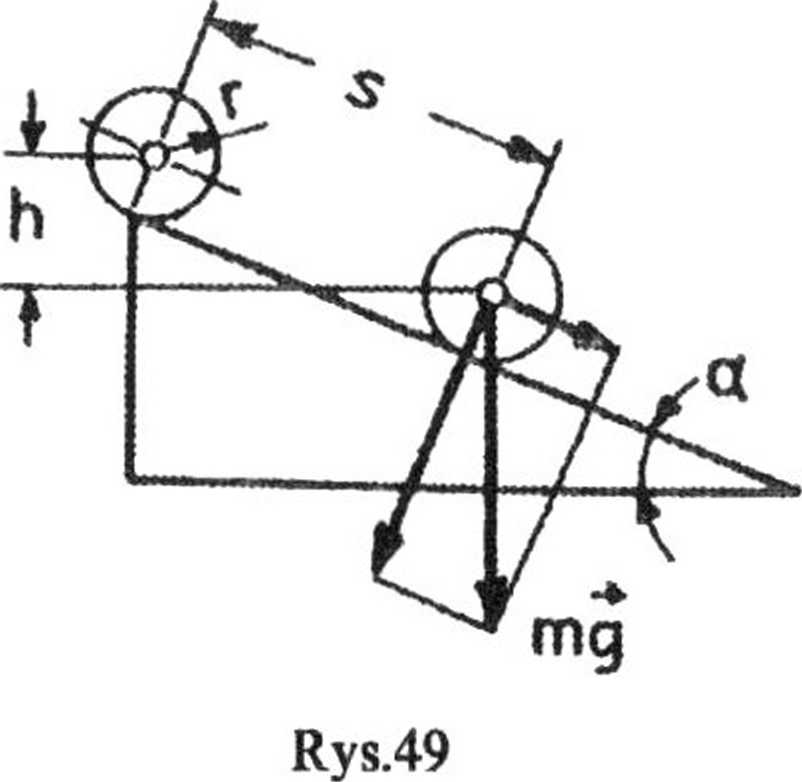
^ mt% = mgs sina,

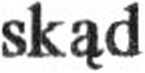
s sina.

Prędkość zsuwania jest więc jednakowa dla obu ciał.

d. Za pomocą a_s można z równań ruchu wyznaczyć tarcie. Wynosi ono

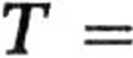
9

więc

dla kuli,

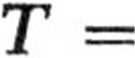
- mg sina

dla walca.

Ruch odbywa się bez poślizgu, gdy

T ^ pN = pmg cosa,

czyli gdy

tga

tga

dla kuli,

dla walca.

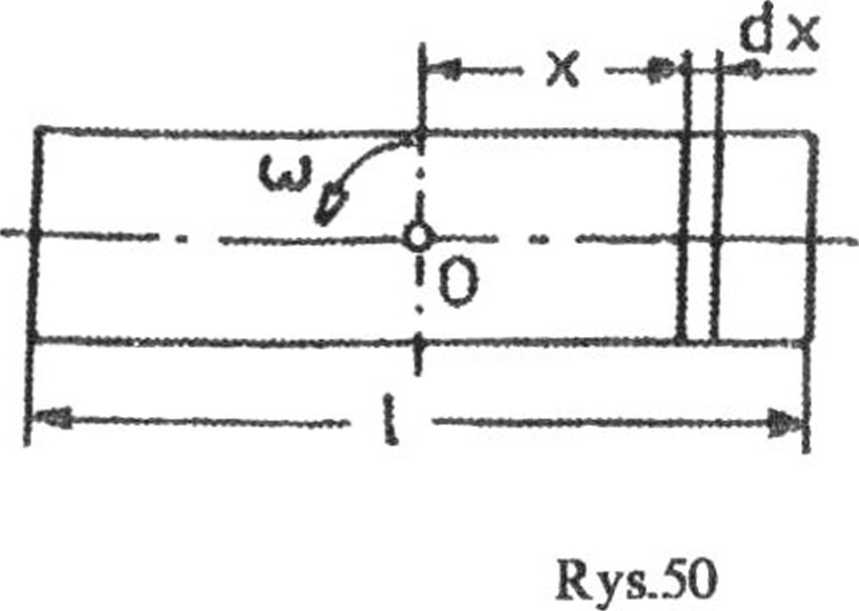
2.92. Elementarna siła odśrodkowa działająca wzdłuż walca (rys.50) jest równa

dF = xcq¹ dm = pSa)¹x dx,

gdzie S jest powierzchnią przekroju walca. Stąd całkowita siła

z

pS(L)

x dx =

0

F

^ pSw²l²,

a odpowiadające jej naprężenie

F

^{p =} ~s =

Podstawiając do tego wzoru wartość granicznego naprężenia p_g znajdujemy aksymalną prędkość kątową obrotu

co

9

pi^:

816 Cs’¹]

2.93. E_k

1

- mr² e² t²

4

= 0,00925 [J]

2.94. Aby cząsteczka znajdująca się na powierzchni cieczy w odległości r od osi obrotu była w równowadze, siła wypadkowa u = (mco²r, —mg) (rys.51)

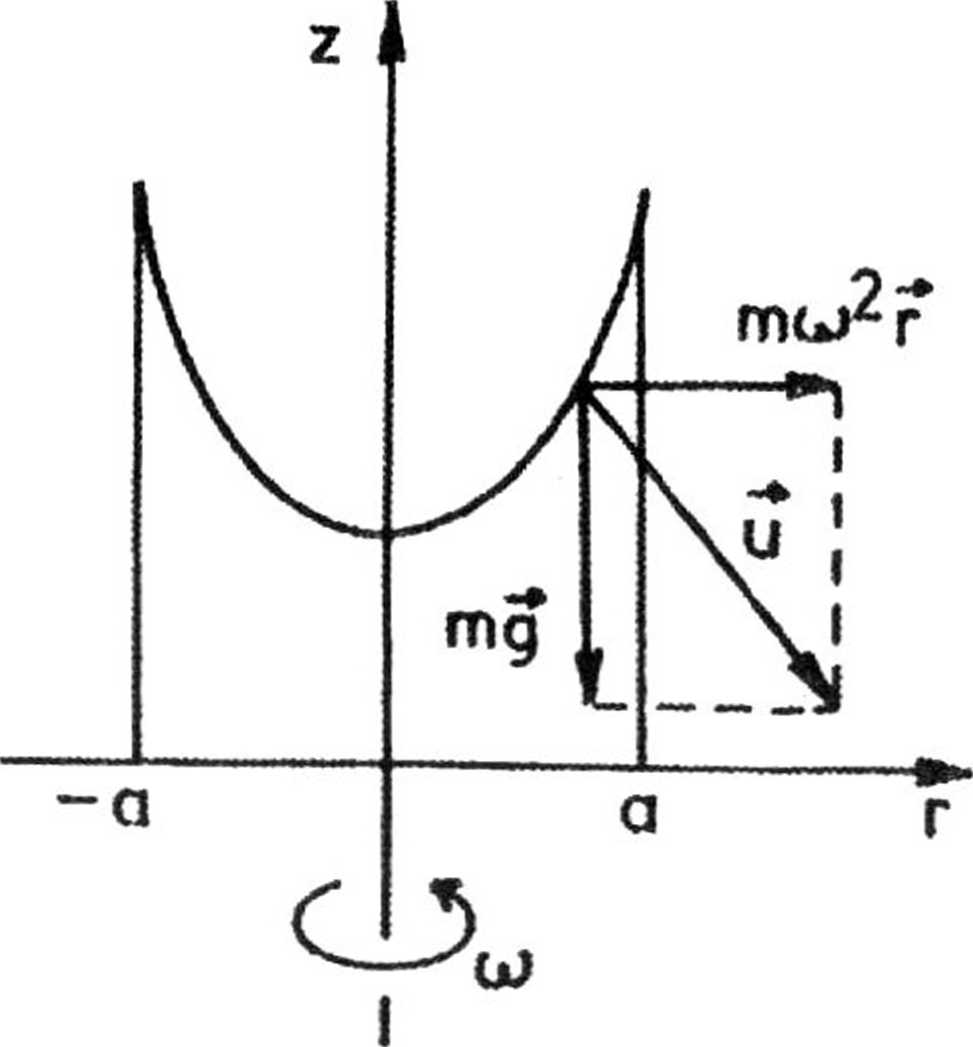
Rys.51

musi być prostopadła do powierzchni. Z równania stycznej i warunku prostopadłości otrzymujemy równanie

= -1,

mg dz

mco²r dr

które po rozdzieleniu zmiennych przybiera postać

co

r dr.

dz =

9

Po elementarnym scałkowaniu mamy równanie kwadratowe określające swobodną powierzchnię cieczy

1

- mg sina