38428 new 78

160    7. Zasady obliczeń wytrzymałościowych śrub

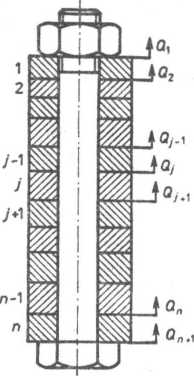
Rys. 7.38. Układ obciążony wieloma siłami roboczymi Qt (i = 1,..., n)

Przyjmijmy, że pod działaniem obciążeń Q, zmniejszenie zacisku wstępnego zachodzi tylko w elemencie j oraz że siła wywołująca to zmniejszenie jest równa X. Wówczas przyrost długości elementu j jest równy

XI

Al, = —= XI,.    (7.90)

^2)? 2)

Odkształcenie to równe jest sumie odkształceń wszystkich pozostałych elementów, w tym również odkształceniu śruby Al_a

i—i    n

M_j = 'ZAl_l+ Z dZ,+dZ₀.    (7.91)

i-1    i—j+l

Suma odkształceń elementów usytuowanych nad elementem j wynosi

i-i

Z Al_t = (Q,-X)V₁ + (Q,+Q^i-X)V₂+.....+

+(Qj+Q*-i+.....+Q2^—-X)li =

j—l    ;—2

= QiS it+Qi-iS i»+.....-\-Qih~xX, u,

1=1    i=l    1=1

więc

i—1    j    k-1    l—l

E AU = Ś Qk    E    E    li.    (7.92)

i=l    k=2    1=1    1=1

Podobnie suma odkształceń    elementów od j+1    do n

S —    (Q, + l + X)l,₊i— (Q, + l + Q, + 2 + X')ll+2 •

i=;+i

(©y+i-ł-ęj+i^*. • •    —

'Qj +1 2 Aj, Q} + 2 2 At ... QnA-n X 2 A{, ł=y+1    ł-j+2    ‘->+1

więc

(7.93)

2 /Ki = - I Q>c 2 A,-X 2

ł=y+l    k=y-fl ł-k I-/+1

Siła rozciągająca śrubę wynikająca z działania sił Q_k (bez uwzględ-

i

nienia siły zacisku wstępnego Q_u) jest równa 2 Q_k—X, a jej odkształ-

k—1

cenie

dl₀ — i„2 Qk A₀x.

k-1

(7.94)

Podstawiając równania (7.92), (7.93) i (7.94) do wzoru (7.91) i łącząc ze wzorem (7.90), otrzymujemy

xi,= 2 Qk*2 K-x2 At- 2 Qk 2 At-x 2 vt-a. 2Q*~AoX,

k-1    ł-1    ł=l k-y+1 ł-k    ł-y+1    k-1

»tąd

x(A₀+ 2 ^+^4- 2 ^) = A₀ 2 Qk + 2 Qk 2    — 2 Qk 2 Ai>

ł-1    ł-y+1    k-1    k-1    i-1    k-y+1 ł-k

więc

y.    k—1    n    n

2 Qk 2    —    2 Qk 2 At

x =

(7.95)

k-1    1=0_k—J+l    1-k

n

2 a,

«=«

Siła rozciągająca śrubę jest zatem równa

J    k—1    n    n

y    y    2 Qk 2 Ai - 2 Qk 2 ^ł

2 Qk - x = 2Qk—^k~^{ł    ł}-“    ⁱ-^te

2 At i-o

J    n    )    k—1    n    n

2 Qk2 a, - 2 Qk 2 ^ + 2 Qk 2 At

k-i    t"Q_k-i    ł—o_k-y+i    t^=k

In

2 At

i-0

k-1    k-1

Ponieważ

2 Qk 2 At— 2 Qk 2 At — 2 Qk 2 At

k-1    ł-0    k=l t-0    k-1 ł-k

oraz

U — Połączenia gwintowe