DSCN1631

It-n ^

160

7. Zasady obliczeń wytrzymałościowych śrub

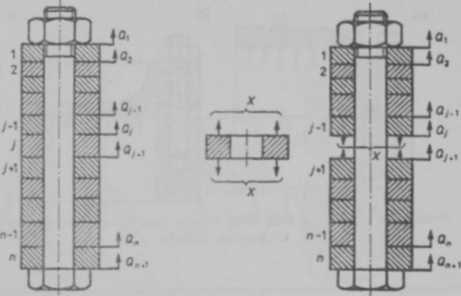
Rys. 7.38. Układ obciążony wieloma siłami roboczymi Qt (i = 1.....n)

Przyjmijmy, że pod działaniem obciążeń Q, zmniejszenie zadaku wstępnego zachodzi tylko w elemencie j oraz że siła wywołująca to zmniejszenie jest równa X. Wówczas przyrost długości elementu j jest równy

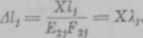
(7.90)

Odkształcenie to równe jest sumie odkształceń wszystkich pozostałych elementów, w tym również odkształceniu śruby

i-i    ł-i+i

(791)

Suma odkształceń elementów usytuowanych nad elementom j wynosi

£ AU = (Q_J-X);._ł_₁+(Q_j+Q_ł-i-X)i_ł__J+.....+

+(Qi+Qł-t+    +Q»-X)l 1 —

więc

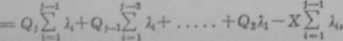
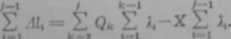
i-1    a—a    i-i    «

(7.92)

Podobnie suma odkształceń elementów od j+1 do n

«l

S /Ht= -(Q_Ju+X)i_łfl-(QiM+Qi_łz+X)i_i,_a-...

1-7+1

7.5. Obliczenia śrub obciążonych osiowo z zaciskiem wstępnym

— (Q|o»+Qjo*+ . .. +Q.+X)i. =

«    n

= “Qi*i2 a,—Q_J+a 2 A,— ... —Q„A_n-x V i

i-y+i    i-j+i

2 /«,=»- £ Qk 2 a,—x 2 i..

i-7+1    *-/+» «-fc    W + l

(7.93)

Siła rozciągająca śrubę wynikająca z działania sił Q_k (bez uwzględnienia siły zacisku wstępnego Q„) jest równa 2^ Q_fc—X, a jej odkształ

cenie

dł₀ = ;.SQ_k-AoX.

(7.94)

Podstawiając równania (7.92), (7.93) i (7.94) do wzoru (7.91) i łącząc ze wzorem (7.90), otrzymujemy

fc—i    M

zi,— Ż <?> £ k-zHi, - £ q> £ t,-x £ 4+1. £ <3,-KX.

a-*    <-•    i=i k-y+i i-k    ł-y-fi    _k-i

stąd

X(ł.+ £ !.+!,+• ± JJ -!.£«,+ £q.£i,- £

_    «-/♦»    k-1    fc-a ł-1    I.-7-H i-k

Więc

2 Qfc 2 Al — 2 Qk Z ii

k-l 1=0_fc-J-i-1 l-k

n

Sa,

im

(7.95)

rozciągająca śrubę jest zatem równa

2 Qk — X = 2 Qk

k—1

i    fc—1    n    n

E Qk 2 A* — E Ok E Ai

fc-1    i-o_fc-y-H    l-k

Ea,

Ptui

eważ

oraz u —

2 Qk 2 A, - S Q_k    2*    Ai    +    E    OiEAi

1    4 0    k-l    i-0    k-y    + l    < k

fn

2 Ai i-o

2 Ok 2 Ai    — 2 Qk    2    Ai    =    2 Qk 2 a,

i-o    k—l    i-0    fc-l    I—fc

^ł*°*fcc«onl»

Bwintowa