30215 MF dodatekA27

272 Podstawy matematyczne Aneks A

Metodę równego podziału stosujemy do określenia z grubsza pierwiastków danego równania. Zauważmy, że przy zwiększaniu dokładności wzrasta znacznie ilość obliczeń.

Metoda interpolacji liniowej

Metoda interpolacji liniowej nazywana jest również regułą falsi lub metodą siecznej. Niech spełnione będą założenia takie jak w przypadku metody równego podziału i niech f(a)<0 i f(b)>0. zamiast dzielić przedział <a,b> na połowy, dzielimy go w stosunku f(a)/f(b), co jest bardziej naturalne.

W konsekwencji otrzymujemy przybliżoną wartość pierwiastka (por. odwrotna metoda interpolacji liniowej wzór A(6.4) dla y₀ =0)

^xi=a-f(ipk^(b-^a) ■    ^A(7-⁶⁾

Następnie stosujemy tę metodę do przedziału wybranego spośród przedziałów <a, x,>, <x,, b>, na którego końcach funkcja f ma dwa różne znaki. W wyniku takiego postępowania otrzymujemy kolejne przybliżenie x₂.

W interpolacji geometrycznej metoda interpolacji liniowej polega na zastąpieniu pierwiastka Xo jego przybliżeniem x, otrzymanym w wyniku przecięcia się siecznej do wykresu funkcji f poprowadzonej przez punkty (a,f(a)); (b,f(b)).

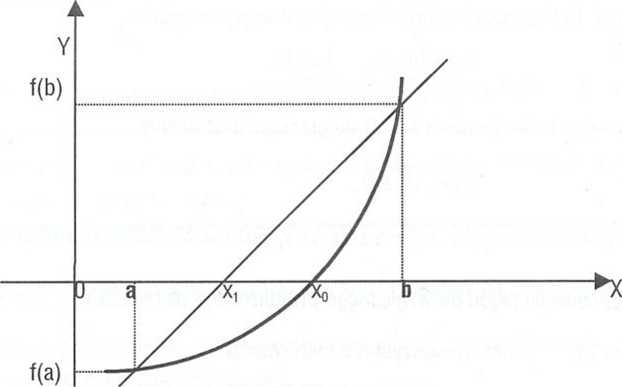
Rys.A.7.1. Metoda interpolacji liniowej wyznaczania pierwiastków równania f(x)=0