40674 str129 (4)

8 2. FUNKCJA BESSELA 129

Neumanna o wskaźniku v na-,0) określoną w następujący

v jest niecatkowitc,

v = n jest całkowite.

?, to funkcję Bessela drugiego teregu:

M

-C+ Yj 1/^w * C /eyf

m = 1

>H2.8), (2.10) i (2.11). Oprócz ice związki:

vnJfz),

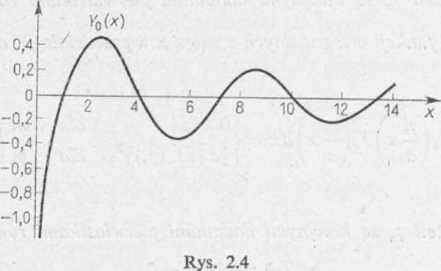
jest na rysunku 2.4.

Definicja 5. Funkcjami Bessela trzeciego rodzaju lub funkcjami Hankela o wskaźniku v nazywamy funkcję zmiennej z w płaszczyźnie z cięciem (—oo,0) o następującej postaci:

(2.15)    H[ⁱ\z) = Jfz)+iYfz),

(2.16)    H[²\z) = Jfz)-iYXz).

Własność 4. Rozwiązaniem ogólnym równania różniczkowego

(2.17)

*

gdzie k / 0, jest funkcja

(2.18)

d²y 1

d?⁺7

dy_

dz

+ k²y = 0,

y — AJ₀(kz) + BY₀(kz).

Rozwiązanie ogólne równania (2.17) można również wyrazić w następującej postaci:

(2.19)

y = AH⁽0^l\kz) + BH^l0¹\kz).

Własność 5. Rozwiązaniem ogólnym równania różniczkowego

(2.20)

gdzie k 0, jest funkcja

(2.21)

d²y 1 dy dz²⁺z dz ⁺

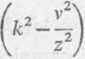
y = o,

y = AJfkz) + BYfkz).

Rozwiązanie ogólne równania (2.20) można również przedstawić w następujących postaciach:

(2.22)    >• = AH⁽f\kz) + BH[²\kz),

(2.23)    y = AJfkz) + BJ^fkz), tylko dla v niecałkowitych.

a _ Wybrane działy matematyki...