32527 str134 (4)

134 2. FUNKCJE SPECJALNE

Definicja 4. Zmodyfikowaną funkcją Bessela rodzaju drugiego o wskaźniku v nazywamy funkcję zmiennej z w płaszczyźnie z cięciem (—oo,0) określoną w następujący sposób:

dla v niecałkowitych, dla v — n całkowitych,

przy założeniu, że |argz| <n.

Własność 3. Jeżeli |argz| <±tt, to między funkcją Kfz) i funkcjami Jfz), y„(z), Il⁽v'\z), H⁽/\z) zachodzą następujące związki:

(3.15)    Kfz) = K__v(z) = ±7t ^^(v+

(3.16)    Kfze^T^‘) = ±±7texp(±±(v± l)7i/)[J_v(z)±iT_v(z)],

(3.17)    K_y(ze*iⁿⁱ) = _±±7iexp(±±(v±l)7t/)//*^2),<1)(z).

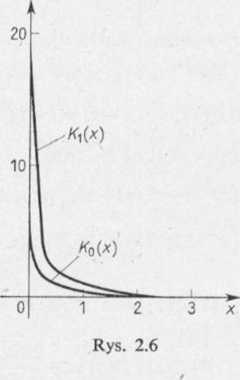
Wykresy funkcji K₀(x) i Kfx), gdzie x jest zmienną rzeczywistą, przedstawione są na rysunku 2.6.

(3.14) Kfz) =

2 sin V7t

Dalsze własności funkcji Kfz) wyrażają następujące zależności:

K_y(ze^m*‘) = e ^vm*^lK_v(z)——--jn7_v(z), m całkowite,

sin vjt

(3.18)

(3.19)	zKfz) = vKv(z) — zKv + 1(z),
(3.20)	zK’fz)= -vKfz)-zKv_f z),
(3.21)	^-[z“^vA:v(z)] = -z^_vKv+1(z), dz

(3.22)
(3.23)	Ifz)K’t(i 00 r r
(3.24)	zKl(kz)dz = ±z^2 L Z 00 /•
(3.25)	zKfkz) Kflz)dz Z

Własność 4. Rozwiązanie

(3.26)

gdzie k ^ 0, jest funkcja

(3.27)

Własność 5. Rozwiązanie

(3.28)

gdzie k # 0, jest funkcja

(3.29)

Dla v niecałkowitych roz w następującej postaci:

(3.30)

Zadania przykładowe

Zadanie 3.1. Wyznaczyć i

(1)

spełniające następujące waru Rozwiązanie. Zgodnie nia (1) jest funkcja

(2)