44621 Rysunek 204

244

l/V ... B. Kinematyka

kątową dotyczy również ruchu zmiennego.

Przyśpieszenie styczne punktu at Av    d(rco)    dcu

a_t =-=--= r- = re

dt At    At

i przyśpieszenie kątowe

_ da>

e —-

At

oraz przyśpieszenie normalne

i>²

a„ —-= rco²

r

Całkowite przyśpieszenie punktu

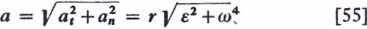
3. Ruch złożony punktu

a.    Ruch bezwzględny, względny i unoszenia

Rozpatrzmy ruchomy układ, w którym porusza się punkt. Układ ten porusza się względem innego układu, który uważamy za nieruchomy. Ruch punktu względem układu ruchomego nazwiemy ruchem względnym, zaś względem układu nieruchomego — ruchem bezwzględnym. Ruch punktu związanego sztywno z układem ruchomym względem układu nieruchomego nazywamy ruchem unoszenia. Odpowiednio mówimy o torze względnym, bezwzględnym i unoszenia, a także o prędkości i przyśpieszeniu względnym, bezwzględnym i unoszenia.

b.    Składanie prędkości

Wyobraźmy sobie, że w ruchomym układzie A porusza się punkt M po torze względnym w (rys. 63) z prędkością względną t>w, a ruchomy układ porusza się względem układu nieruchomego B. Punkt M, gdyby był nieruchomy względem układu ruchomego A, poruszałby się po torze unoszenia u z prędkością unoszenia t;_M. Punkt M względem układu nieruchomego B porusza się po torze bezwzględnym b z prędkością bezwzględną v_b.

Rys. 63

Prędkość bezwzględna ' v_b jest sumą wektorową (geometryczną) prędkości względnej v_w i prędkości unoszenia v_u

v_b = v_w+v_u    [56]

A zatem wartość prędkości bezwzględnej odpowiada długości przekątnej równole-głoboku zbudowanego na prędkości względnej i unoszenia

v_b = }/    + v² + 2v_wv_ucosoi    [57]

gdzie a — kąt zawarty między wektorami v_w i

Przykład. Klin K o kącie a = 30° porusza się po płaszczyźnie ze stałą prędkością unoszenia v_u = = 12 m/min (rys. 64). O klin opiera się rolka z zamocowanym prętem AB przesuwającym się w pionowej prowadnicy. Ruch pręta AB można uważać za ruch bezwzględny (względem nieruchomego podłoża), wynikający z ruchu klina (unoszenia) i ruchu rolki po powierzchni klina (względnego). Określić prędkość względną przesuwania się rolki po klinie v_w oraz prędkość bezwzględną przesuwu pręta v_b.

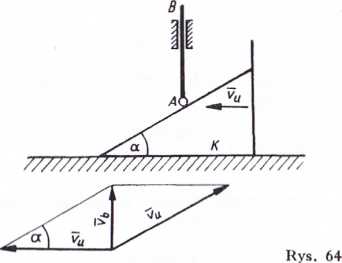
Ponieważ kierunki prędkości bezwzględnej v_b i względnej v_w są określone, można więc zbudować, mając znaną prędkość unoszenia v_u, równoległobok prędkości, z którego wyznaczamy

^vb “ v_utga =■ 12 tg30® = 6,93 m/min

c. Składanie przyśpieszeń

Przyśpieszenie bezwzględne punktu w ruchu złożonym a_b stanowi sumę geometryczną trzech przyśpieszeń, a mianowicie: przyśpieszenia względnego a_Wf przyśpieszenia unoszenia a_u oraz przyśpieszenia Coriolisa

d_c

a_b = a_w+a_u+a_c    [58]

Jeżeli tor względny oraz tor unoszenia są torami krzywoliniowymi, odpowiednie przyśpieszenia są sumami geometrycznymi przyśpieszenia normalnego i stycznego, a więc

Of) ⁼ a_wn "H &wt    "b^iłf “ł“#c    [59]

Przyśpieszenie Coriolisa a_c występuje w tych przypadkach, gdy ruch unoszenia jest ruchem obrotowym. Wektorowo przyśpieszenie to można wyrazić w postaci podwójnego iloczynu wektorowego prędkości względnej Vw i prędkości kątowej obrotowego ruchu unoszenia d)

a_c = 2co X v_w    [60]

Wektor prędkości kątowej (D leży na osi obrotu i jest skierowany w stronę, z której

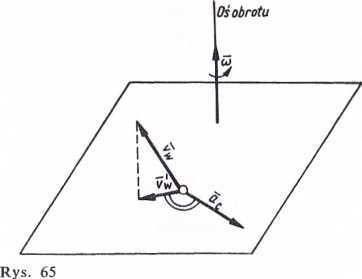
widać obrót o kierunku przeciwnym do kierunku obrotu wskazówek zegara. Wartość przyśpieszenia Coriolisa

ac = 2covwsin(dj, vw)	[61]
lub
ac — 2 cov„	[62]

gdzie — miara rzutu wektora v_w na płaszczyznę prostopadłą do osi obrotu (rys. 65).

Kierunek przyśpieszenia Coriolisa odpowiada obróconemu o 90°, zgodnie z kierunkiem obrotowego ruchu unoszenia, rzutowi prędkości względnej v'_w. Jak z tego wynika, przyśpieszenie Coriolisa jest równe zeru, gdy kierunek ruchu względnego jest równoległy do osi obrotu.

Jeżeli punkt porusza się w płaszczyźnie prostopadłej do osi, przyśpieszenie Coriolisa wynosi

a_c = 2 oov_w

Przykład. Pręt AB obraca się ze stałą prędkością kątową to — 2 1/s wokół osi AO, zataczając końcem B okrąg koła o promieniu r = 3 m (rys. 66). Wysokość AO = h = 4 m. Wzdłuż pręta w kierunku punktu A porusza się ruchem jednostajnym punkt M, przy czym jego prędkość v_w = 3 m/s. Obliczyć prędkość i przyśpieszenie bezwzględne punktu M w chwili, gdy znajduje się on na wysokości hl3 nad punktem O. Układ ruchomy wiążemy z obracającym się prętem. Prędkość poruszającego się po pręcie punktu M jest to prędkość ruchu względnego. Tak więc v_w = 3 m/s. Prędkość unoszenia v_u wynika z prędkości to

2 2

^vu = r_Mto = — _rto = y • 3 • 2 = 4 m/s

Prędkość bezwzględna

v_b =    = V4²+3² = 5 m/s

Przyśpieszenie względne a_w = 0 (ruch jednostajny) ; przy ruchu obrotowym ze stałą prędkością kątową składowa styczna przyśpieszenia jest równa zeru.

A

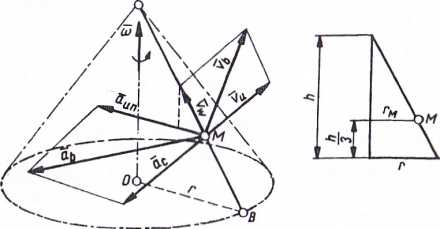
Rys. 66