Rysunek 201

238 l/V ... B. Kinematyka

ona określenie położenia punktów należących do ciała w dowolnej chwili, nie zajmuje się natomiast przyczynami wywołującymi ruch.

1. Ruch punktu, tor, równania ruchu

Punkt znajduje się w ruchu, jeżeli jego położenie w stosunku do pewnego układu odniesienia zmienia się w miarę upływu czasu. Ruch jest więc pojęciem względnym, gdyż jest zależny od przyjęcia układu odniesienia. Zazwyczaj za nieruchomy układ odniesienia uważamy układ związany z Ziemią.

Torem punktu nazywamy linię, po której porusza się punkt w przestrzeni. Tor punktu może być linią płaską lub przestrzenną. Szczególnym przypadkiem ruchu po torze płaskim jest ruch wzdłuż linii prostej.

Jeżeli punkt M porusza się względem nieruchomego układu współrzędnych po pewnej linii (rys. 47), to dla określenia tego ruchu niezbędne jest podanie zależności pomiędzy współrzędnymi tego punktu a czasem, zwanych równaniami parametrycznymi ruchu

y    = /,(t) [29?

Przez wyrugowanie z tego układu równań czasu można określić krzywą, po której porusza się punkt, czyli znaleźć równanie toru.

Możliwe jest również otrzymanie zależności między drogą przebytą przez punkt a czasem w postaci równania ruchu punktu

s = f(t)    [30]

W chwili t = t₀ *= 0 (rys. 48) punkt znajduje się w odległości s₀ od pewnego stałego punktu O na torze ruchu zwanego początkiem drogi, a w chwili t_t punkt jest oddalony o s_t od tego punktu itd.

Równanie ruchu punktu można przedstawić bezpośrednio na wykresie, na którym odkłada się długości przebytej drogi w funkcji czasu (rys. 49).

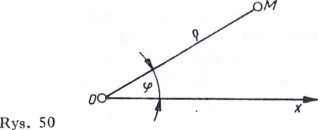
Równanie ruchu punktu można też przedstawić we współrzędnych biegunowych. Położenie punktu M na płaszczyźnie można określić za pomocą odległości od pewnego stałego punktu O, czyli długością promienia wodzącego q, oraz kąta 97, który tworzy promień wodzący z pewną stałą prostą x (rys. 50). Jeżeli obie te wielkości przedstawimy w funkcji czasu t_y to otrzymamy równania ruchu w płaskich współrzędnych biegunowych

q i fi(0;    = f2(0    Pi]

Cl

Ci

= C otrzymamy równanie krzy-

Przykład. Określić tor punktu jeśli dane są parametryczne równania ruchu

x — 2+41;    y = 34-2t

Rugując parametr t znajdujemy równanie toru

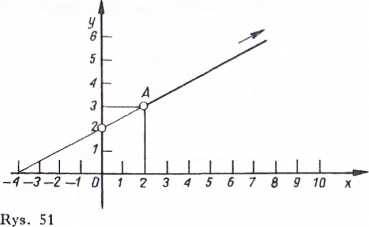
y * ‘2’*+2 będące równaniem linii prostej (rys.

51), przy czym poruszający się punkt rozpoczyna ruch od punktu A o współrzędnych x = 2, y =3, w którym znajduje się w chwili t = 0.

Przykład. Należy wyznaczyć tor punktu, którego ruch jest opisany za pomocą współrzędnych biegunowych

r = Cit; <p = C₂t gdzie C_t i C₂ — stałe.

Rugując parametr t otrzymuje się równanie toru w postaci

oznaczając wej zwanej spiralą Archimedesa r m C<p

2. Prędkość i przyśpieszenie punktu

a. Prędkość w ruchu jednostajnym

Punkt porusza się ruchem jednostajnym jeżeli w ciągu jednakowych przedziałów czasu przebywa takie same drogi. Jeżeli w chwili i = 0 punkt znajdował się w odległości s₀ od pewnego stałego punktu O leżącego na torze, zaś w chwili t odległość ta wynosiła s (rys. 52), to

Rys. 52 równanie ruchu punktu poruszającego się ruchem jednostajnym ma postać

s = s₀ + vt    [32]

gdzie v—wartość bezwzględna (moduł)¹* prędkości ruchu jednostajnego.

Z zależności [32] wynika, że

s — s₀

v =--

t

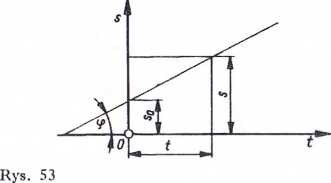
czyli prędkość ruchu jednostajnego jest równa ilorazowi długości przebytej drogi i czasu trwania tego ruchu. Interpretacją geometryczną zależności [32] jest linia prosta (rys. 53), której tangens kąta nachylenia odpowiada prędkości ruchu (przy uwzględnieniu przyjętych podzia-łek wykresu).

Podstawową jednostką prędkości jest 1 m/s, pochodnymi — 1 km/h, 1 m/min itp. Prędkość jest wielkością wektorową, ponieważ dla jej określenia oprócz wartości jest niezbędna znajomość jej kierunku oraz zwrotu.

b. Prędkość w ruchu zmiennym

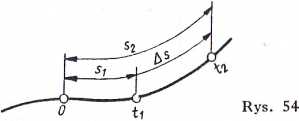
Punkt porusza się ruchem zmiennym (niejednostajnym) jeżeli w ciągu jednakowych przedziałów czasu przebywa po swym torze różne drogi. Jeżeli w chwili ti punkt znajdował się w odległości $1, zaś w chwili t₂ w odległości s₂ od nieruchomego punktu O (rys. 54), to

o W niektórych przypadkach przy rozpatrywaniu prędkości i przyśpieszeń pominięto wyraz wartość (moduł), co jest skrótem przy skal arowym określaniu tych wielkości.