Rysunek 205

246 l/V ... B. Kinematyka

246 l/V ... B. Kinematyka

Przyśpieszenie unoszenia — składowa normalna

a_un = <*>²r_M = a>2 • y r = 22 * y • 3 = 8 m/s²

Wektory <3 i v_w tworzą między sobą kąt, którego sinus wynosi 3/5 (patrz rysunek — jest to sinus połowy kąta wierzchołkowego stożka).

Przyśpieszenie Coriolisa punktu M wyniesie

a_c — 2«w_wsin(o>, v_w) = 2 • 2 • 3 • y = 7,2 m/s²

Ostatecznie przyśpieszenie bezwzględne punktu M

a_b = Val_n+al = ^8^a+7,2^a = 10,76 m/s²

Kierunki prędkości i przyśpieszenia są podane na rysunku.

4. Podstawowe ruchy ciała sztywnego

a. Ruch postępowy

Ruchem postępowym ciała sztywnego nazywamy taki ruch, w czasie którego dowolna linia prosta łącząca dwa punkty ciała porusza się do siebie równolegle. Ruch postępowy wykonuje na przykład nadwozie wagonu toczącego się po prostym torze, ruchem postępowym będzie również ruch łącznika AB (rys. 67) łączącego jednakowe korby O^A i 0₂B obracające się wokół punktów 01 i O₂.

Rys. 67

Jeżeli pewne ciało jest sztywno związane z elementem, o którym wiemy, że wykonuje ruch postępowy, to ciało to również znajduje się w ruchu postępowym. Jeżeli na przykład z łącznikiem AB zwiążemy sztywny trójkąt ABC (rys. 68), to również będzie on wykonywać ruch postępowy.

C

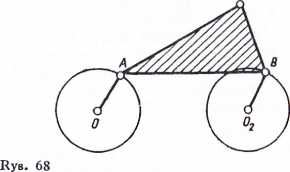
Wszystkie punkty ciała poruszające się ruchem postępowym mają jednakowe tory ruchu i w ciągu tego samego okresu przebywają takie same drogi. Wynika stąd, że prędkości wszystkich punktów mają w danej chwili tę samą wartość i ten sam kierunek. Analogicznie można stwierdzić, że przyśpieszenia wszystkich punktów ciała mają tę samą wartość i kierunek. A zatem dla określenia ruchu dowolnego ciała znajdującego się w ruchu postępowym wystarczy zbadać ruch jednego punktu należącego do tego ciała.

Szczególnym przypadkiem ruchu postępowego jest ruch prostoliniowy (translacja lub przesunięcie), w czasie którego wszystkie punkty ciała poruszają się po prostych równoległych.

b. Ruch obrotowy wokół stałej osi

Ciało sztywne wykonuje ruch obrotowy, jeżeli dwa punkty należące do tego ciała są nieruchome. Punkty te określają wówczas oś obrotu. Nieruchome są także wszystkie punkty leżące na tej osi.

Rozpatrzmy stożek ścięty obracający się wokół osi 0i0₂ (rys. 69). Ruch obrotowy charakteryzuje obrót płaszczyzny przechodzącej prze oś obrotu. Płaszczyzna 0₁AB0₂ po czasie t obróci się o kąt (p i zajmie położenie 0₁^4'S'0₂. O kąt <p obrócą się więc wszystkie punkty ciała.

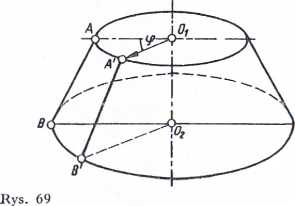
A zatem do określenia ruchu obrotowego wokół stałej osi wystarczy znać ruch dowolnego punktu ciała nie leżącego na osi obrotu.

Prędkości poszczególnych punktów są skierowane stycznie do torów, a zatem są prostopadłe do promieni łączących te punkty z osią obrotu.

(o

4 n 1/s

nn

[64]

Prędkość ruchu obrotowego ciała określa się przez podanie prędkości kątowej a>, przy czym w przypadku ogólnym prędkość

Aa?    d a?

a? = lim —j- = —    [63]

At-*o At    dt

gdzie Aq> — kąt obrotu ciała w czasie At. Oczywiście, przy ruchu obrotowym jednostajnym co = const.

Jeżeli liczba obrotów ciała w ciągu minuty wynosi n, to prędkość kątowa

q?    2 nn    nn 1

t 60    30 s

Zależności określające prędkość i przyśpieszenie punktu 'wykonującego ruch jednostajny i zmienny po okręgu koła można bez żadnych zmian stosować do określania prędkości i przyśpieszeń punktów ciała znajdującego się w ruchu obrotowym wokół osi.

Przykład. Koło pasowe o średnicy D = lm obraca się jednostajnie wykonując n = 120 obr/min. Określić prędkość i przyśpieszenie punktów leżących na obwodzie koła Prędkość kątowa

n' 120 30

Ponieważ w = const, więc przyśpieszenie kątowe e = 0. Prędkość obwodowa

v roi — (a — 0,5 * 4n — 2n — 6,28 m/s

Przyśpieszenie styczne a_t — re = Q

Przyśpieszenie normalne a_n — r<o² = 0,5 * (4?r)² = 79 m/s²

c. Ruch płaski

Ruchem płaskim ciała sztywnego nazywamy taki ruch, podczas którego wszystkie punkty tego ciała poruszają się w płaszczyznach równoległych do pewnej stałej płaszczyzny. Wszystkie punkty ciała leżące na prostopadłej do tej płaszczyzny mają te same tory i prędkości, a zatem przy rozpatrywaniu ruchu płaskiego ciała sztywnego wystarczy rozpatrywać ruch płaskiej figury powstałej przez przecięcie danego ciała płaszczyzną równoległą do wspomnianej stałej płaszczyzny. Dla zbadania tego ruchu wystarczy określenie parametrów ruchu dwóch dowolnych punktów figury płaskiej.

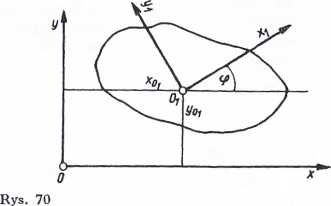
Każdy ruch płaski można uważać za ruch postępowy figury płaskiej z jednoczesnym jej obrotem wokół dowołnie obranego punktu. Załóżmy, że figura płaska S (rys. 70) porusza się ruchem płaskim względem nieruchomego układu współrzędnych xy. W punkcie O_t tej figury umieszczamy układ x±yi związany z ruchomą figurą. Ruch płaskiej figury (a więc i ciała sztywnego wykonującego ruch płaski) będzie określony przez trzy równania

*oi = IM) y<n =    <P = f*(t)

[65]

gdzie: ac₀i i yoi— współrzędne dowolnego punktu (bieguna) figury (początku współrzędnych układu ruchomego), tp — kąt obrotu układu ruchomego w stosunku do układu nieruchomego.

Pierwsze dwie zależności określają ruch postępowy; zależą one od wyboru bieguna Oi. Trzecia zależność określa ruch obrotowy wokół bieguna O i, przy czym nie zależy ona od wyboru bieguna.

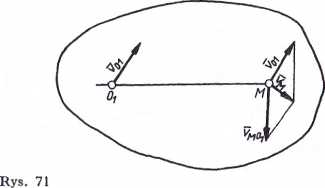
Prędkość dowolnego punktu figury w ruchu płaskim można znaleźć wykreślnie jako sumę geometryczną prędkości bieguna (prędkości unoszenia) i prędkości w ruchu obrotowym wokół bieguna (prędkości względnej).

Jeżeli jest dana prędkość punktu Oi wynosząca tioi (rys. 71) i prędkość

17 Mały poradnik mechanika t. I