Rysunek 206

•I i!

•I i!

248

l/Y ... B. Kinematyka

i i 11

jt' ijf

lii

kątowa co wokół tego punktu, to prędkość vm punktu M wyniesie

= 5?o, ^_    [66]

gdzie vmo₁ ~ ⁴⁰ * Oi Af— prędkość w ruchu obrotowym punktu M względem punktu Oi.

Często przy badaniu ruchu płaskiego znajduje zastosowanie twierdzenie o ruchu prostej:    rzuty prędkości dwóch

dowolnych punktów poruszającej się prostej na tę prostą są sobie równe (rys. 72)

v'_A = v'_B

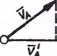
Rys. 72

W każdym ruchu płaskim (z wyłączeniem ruchu postępowego, który jest przypadkiem szczególnym ruchu płaskiego) istnieje w danej chwili punkt, którego prędkość jest równa zeru. Punkt ten nazywamy chwilowym środkiem obrotu. Ruch płaski można zatem uważać za szereg chwilowych obrotów wokół zmieniającego się w sposób ciągły środka obrotu. Jeżeli więc określony jest chwilowy środek obrotu i prędkość kątowa obrotu wokół niego, to prędkość każdego punktu ciała obliczymy jako iloczyn tej prędkości kątowej i odległości punktu od tego środka.

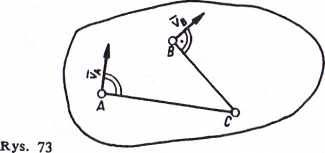
Położenie chwilowego środka obrotu, w przypadku gdy są określone kierunki prędkości dwóch punktów ciała, wyznaczamy prowadząc prostopadłe do tych prędkości (rys. 73). Na ich przecięciu leży chwilowy środek obrotu C. Jeżeli natomiast kierunki prędkości są równoległe, a ich wartości są znane, wówczas położenie określonego środka obrotu wyznaczamy w sposób przedstawiony na rys. 74.

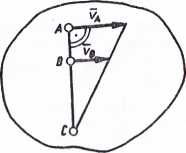
Rys. 74

Miejsce geometryczne chwilowych środków obrotu na płaszczyźnie stałej nazywamy centroidą (polodią) stałą, natomiast miejsce geometryczne chwilowych środków obrotu n,a płaszczyźnie związanej z poruszającą się figurą płaską nazywamy centroidą (polodią) ruchomą. Podczas ruchu płaskiego następuje toczenie się bez poślizgu centroidy ruchomej po centroidzie stałej.

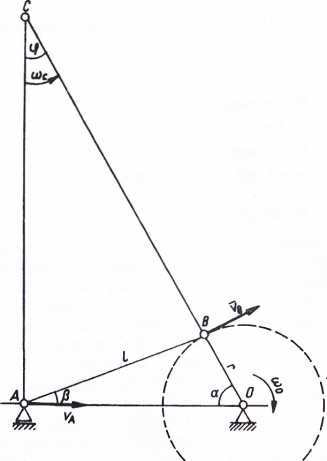
Przykład. W mechanizmie korbowym przedstawionym na rys. 75 jest dana prędkość kątowa korby (o_a = 5 l/s, promień korby r — 0,5 m, długość korbowodu l — 1,2 m. Określić dla położenia korby a = 60° prędkość vg czopa korbowego B, położenie chwilowego środka obrotu C korbowodu, jego chwilową prędkość kątową <o_c oraz prędkość Vą wodzika A.

Prędkość punktu B ^VB — °*o^r = 5 * 0,5 = 2,5 m/s

Rys. 75

0,5 * sin 60°

m

0,361;

1,37

8in30°

2,74 m

Chwilowy środek obrotu C korbowodu leży na przecięciu prostych prostopadłych do kierunków prędkości i v_B.

Znajdujemy kąt /3

.    r sin oc

sinp = —-—

P = 21°10^/

oraz

AO -»/cos0+rcosoc = 1,2*0,932+0,5*0,5 w. =» 1,37 m

OC = -4^-sin <p

Stąd odległość punktu B od chwilowego środka obrotu C

CB = OC-r m 2,74-0,5 gj 2,24 m Chwilowa prędkość kątowa korbowodu v_B 2,5

®^c " CB “ 2,24 ^{= 1,12 1/8}

Odległość punktu ^4 od chwilowego iśrodka obrotu

CA = OCcosę> = 2,74 *0,866 = 2,37 m Prędkość wodzika

^VA “ *°cC-A ~ 1,12*2,37 = 2,65 m/s

d. Ruch kulisty

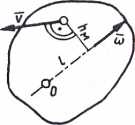
Ruchem kulistym nazywamy taki ruch ciała sztywnego, w którym jeden punkt ciała jest nieruchomy. W ruchu tym wszystkie punkty poruszają się po powierzchniach współśrodkowych kul, których środkiem jest ów nieruchomy punkt. Ruch kulisty ciała można w danej chwili uważać za obrót wokół pewnej osi, zwanej chwilową osią obrotu, przechodzącą przez nieruchomy punkt.

Rys. 76

Jeżeli ciało wykonuje ruch kulisty ,vokół punktu O (rys. 76) i w danej chwili osią obrotu jest oś /, to prędkość punktu M ciała jest określona iloczynem

v = (oh_M

gdzie: co — chwilowa prędkość kątowa ciała, hj^ — odległość punktu M od osi 1.

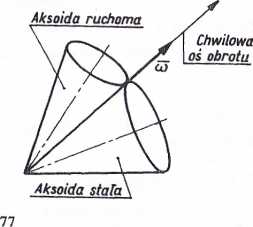
Miejscem geometrycznym chwilowych osi obrotu w układzie nieruchomym jest pewna powierzchnia stożkowa zwana aksoidą stalą, zaś w układzie związanym z ruchomym ciałem — aksoidą ruchomą (rys. 77). Podczas ruchu kulistego następuje toczenie się bez poślizgu aksoidy ruchomej po aksoidzie stałej.

C. Dynamika

Dynamika zajmuje się badaniem ruchu ciał. Jednakże w odróżnieniu od kinematyki, nie zajmuje się samym opisem ruchu, lecz badaniem zależności między ruchem a przyczynami powodującymi ten ruch, czyli między siłami działającymi na rozpatrywane ciała. Zależności te umożliwiają bądź określenie sił występujących przy danym ruchu ciał, bądź też określenie parametrów ruchu powstającego w wyniku działania danych sił.

1. Dynamika punktu materialnego

a. Podstawowe prawa dynamiki

Podstawowymi prawami dynamiki (klasycznej) są prawa Newtona. W odniesieniu do punktu materialnego prawa te można sformułować jak następuje.

I    prawo Newtona: punkt materialny, na który nie działa żadna siła lub działa układ sił równoważny zeru, porusza się ruchem jednostajnym po linii prostej lub też znajduje się w spoczynku (tzw. prawo bezwładności).

II    prawo Newtona: siła P, działając na swobodny punkt materialny, nadaje mu przyspieszenie a proporcjonalne do

17*