Rysunek 203

242 l/V ... B. Kinematyka

242 l/V ... B. Kinematyka

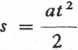
[47b]

s

s—vt

t²

= 2

a

160 m/min²

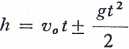
[48b]

ko we wartości w ciągu jednakowych przedziałów czasu, czyli jest to ruch o stałym przyśpieszeniu (lub opóźnieniu). Zatem jeżeli prędkość w chwili t = 0 wynosi v₀, to prędkość w chwili t wyniesie

v = v₀+at

gdzie a — przyspieszenie punktu.

Zależność powyższą można przedstawić wykreślnie (rys. 60). Tangens kąta nachylenia prostej względem osi t odpowiada przyśpieszeniu a.

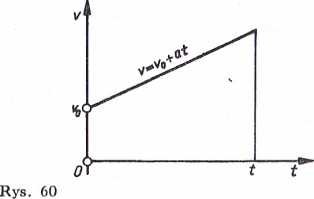
Drogę przebytą w ruchu jednostajnie zmiennym przyśpieszonym lub opóźnionym w czasie t określa zależność

at²

s — v„t+-    [46] gdzie znak dodatni oznacza przyśpieszenie dodatnie, a znak ujemny —■ przyśpieszenie ujemne.

Jeżeli prędkość początkowa v₀ jest równa zeru, wówczas droga przebyta w ruchu jednostajnie zmiennym [47a]

Ponieważ v = at_y więc

v² 2 a

skąd otrzymujemy zależność określającą prędkość końcową jako

V = j/2^7    [47c]

Przykład. Pociąg w chwili wjazdu na odcinek trasy ze spadkiem rozwijał prędkość 60 km/h. Odcinek ten, o długości 3 km, przebył w ciągu 2,5 minuty. Zakładając, źe ruch pociągu był jednostajnie przyśpieszony określić jego prędkość po przebyciu wspomnianego odcinka.

Prędkość początkowa v₀ — 60 km/h = "■ 1000 m/min.

Rozwiązując zależność [46] względem a, znajdziemy przyśpieszenie pociągu 3000-1000*2,5

2,5²

Prędkość końcowa wyniesie v = 1000 +160 X X 2,5 = 1400 m/min = 84 km/h

2) Ruch pionowy ciała. Ruch ten jest szczególnym przypadkiem ruchu jednostajnie zmiennego (przy założeniu, że opory spowodowane tarciem można pominąć), przy czym stałe przyśpieszenie jest równe ziemskiemu przyśpieszeniu sił ciężkości g (g = 9,81 m/s²).

Drogę w ruchu jednostajnie przyśpieszonym ciała spadającego lub wyrzuconego w górę_} którego prędkość początkowa wynosiła v_Qy można określić na podstawie wzoru [46]'za pomocą zależności [48a] gdzie znak plus oznacza przyśpieszenie g dodatnie (ciało spadające), a znak minus—przyśpieszenie g ujemne (ciało wyrzucone w górę).

Wzór [48a] można wyrazić w postaci

vl ±v²

2g

gdzie v — prędkość po czasie t.

Wysokość rzutu h ciała rzuconego pionowo w górę z prędkością początkową v₀ otrzymamy, gdy w ostatniej zależności przyjmiemy v = 0 vl

h — -r—    [49]

2g

Ze wzoru [49] wynika, iż niezbędna dla osiągnięcia wysokość h prędkość początkowa wynosi

v_Q = iflgh    [50]

Droga przy swobodnym spadku dala (z prędkością początkową v₀ — 0), zgodnie ze wzorem [48a] przyjmie postać

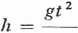
2

a przy v — gt v²

h =-

2g

Stąd prędkość ciała spadającego swobodnie z wysokości h

v — }/2gh

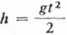
9,81 *6² 2

Prędkość

[51]

[52]

Przykład. Stwierdzono, że czas spadania kamienia wyniósł 6 sekund. Z jakiej wysokości rzucono kamień i jaka była jego prędkość w chwili uderzenia? Wysokość

= 176,6 m

v - gt - 9,81 • 6 = 58,9 m/s

3) Rzut ukośny. Przy wyrzuceniu ciała z prędkością v₉ pod kątem <x do poziomu (przy pominięciu oporu powietrza) ruch jego w układzie współrzędnych x, y będzie odbywać się zgodnie z następującymi równaniami (rys. 61)

gt²

x = v₀t cosa; y =v₀tsm(x---

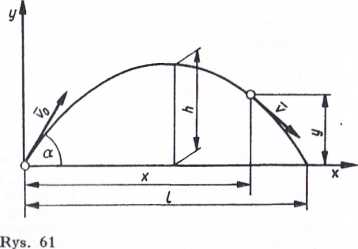
Po wyrugowaniu t zależność pomiędzy wysokością y i odległością x od punktu wyrzutu przyjmie postać

gx²

y = xtga--—~-—

2,v₀ cos a

Maksymalna wysokość przy danym kącie <x

vl sin²<x

ymax — h ⁼    —

2g

zaś maksymalna odległość (doniosłość rzutu) przy danym kącie <x

v²s\nl(x

Xmax = l = - [53]

g

Doniosłość rzutu / przy danej prędkości v₀ jest największa przy <x = 45°

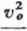
g

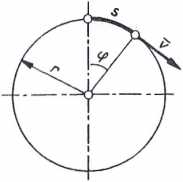
4) Ruch jednostajny po okręgu koła. W ruchu jednostajnym punktu po okręgu koła prędkość v_y nazywana również prędkością obwodową, jest stała, natomiast kierunek ulega stałej zmianie.

Rys. 62

Droga liniowa mierzona po łuku (rys. 62) wynosi

s = vt

Drodze liniowej s odpowiada droga kątowa <p, którą zakreśla promień wodzący poruszającego się punktu

s

*P ~ — r

Prędkością kątową punktu co nazywamy drogę kątową (w radianach), którą przebywa punkt w jednostce czasu

V

co = — t

W rozpatrywanym ruchu prędkość kątowa jest stała.

Ponieważ s = vt = r<p_f więc rq>

v = ——- = rco    [54]

t

Zgodnie z [43] i [44] przyśpieszenie styczne rozpatrywanego ruchu a_t — 0, zaś przyśpieszenie normalne (dośrodkowe)

V²    ₂

a_n =-= ra> = const

r

A zatem całkowite przyśpieszenie ma stałą wartość a = rco² i jest stale zwrócone ku środkowi koła.

5) Ruch zmienny po okręgu koła. W ruchu zmiennym po okręgu koła zmienia się wektor prędkości v (prędkość obwodowa), a przez to również prędkość kątowa co. Zależność [54] między prędkością liniową (obwodową) a prędkością