026 027 2

26 Programowanie liniowe

Rysunek 1.3    Rysunek 1.4

i «2		/~ 4x, = 16	1 Xj	x,>0
4x, <16	I I I
0(0.0)		(4,0) x,	0(0,0)	*1

Rysunek 1.5

x₂

0(0.0)

Z kolei znajdujemy obszar będący części;) wspólną półpłaszczyzn wyznaczonych przez kolejne warunki ograniczające (rys. 1.6).

Rysunek 1.6

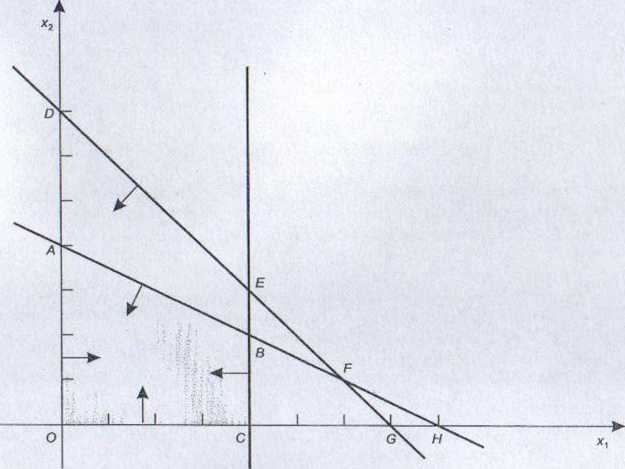
Na rysunku L.6 pokazano, że ograniczenie (1.1), dotyczące dostępności środka <

S|, nie jest aktywne przy wyznaczaniu części wspólnej. Oznacza to, że dla każdego ( planu dopuszczalnego ograniczenie to będzie spełnione jako nierówność ostra. /    .

Jednocześnie każdy punkt czworoboku O ABC jest rozwiązaniem dopuszczalnym zadania programowania produkcji.

1.2.3. Warstwice funkcji celu

Zajmiemy się teraz znalezieniem rozwiązania optymalnego, dla którego wartość funkcji celu jest największa. W dalszych rozważaniach geometrycznych wykorzystamy metodę prób i błędów. Ustalmy pewną wartość zysku, np. wartość 6, i zapytajmy, czy istnieje przynajmniej jedno rozwiązanie dopuszczalne, które pozwoli nam zrealizować ten zysk. Rysując prostą 2jt, + 3x₂ = 6 (czyli warstwicę funkcji celu dającą zysk 6), stwierdzamy, że istnieje nieskończenie wiele punktów tej prostej leżących wewnątrz obszaru dopuszczalnego (rys. 1.7). 'Pak więc odpowiedź na pytanie dotyczące istnienia rozwiązania dopuszczalnego dającego wartość 6 jest pozytywna.

Podejmiemy teraz próbę znalezienia lepszych rozwiązań. Wybieramy większą wartość zysku, np. wartość 12, i znajdujemy odpowiadającą jej warstwicę funkcji celu, rysując prostą 2x_[ + '$x₂=\2. Ponownie stwierdzamy, że istnieją wspólne