086 087 2

86 Programowanie liniowe

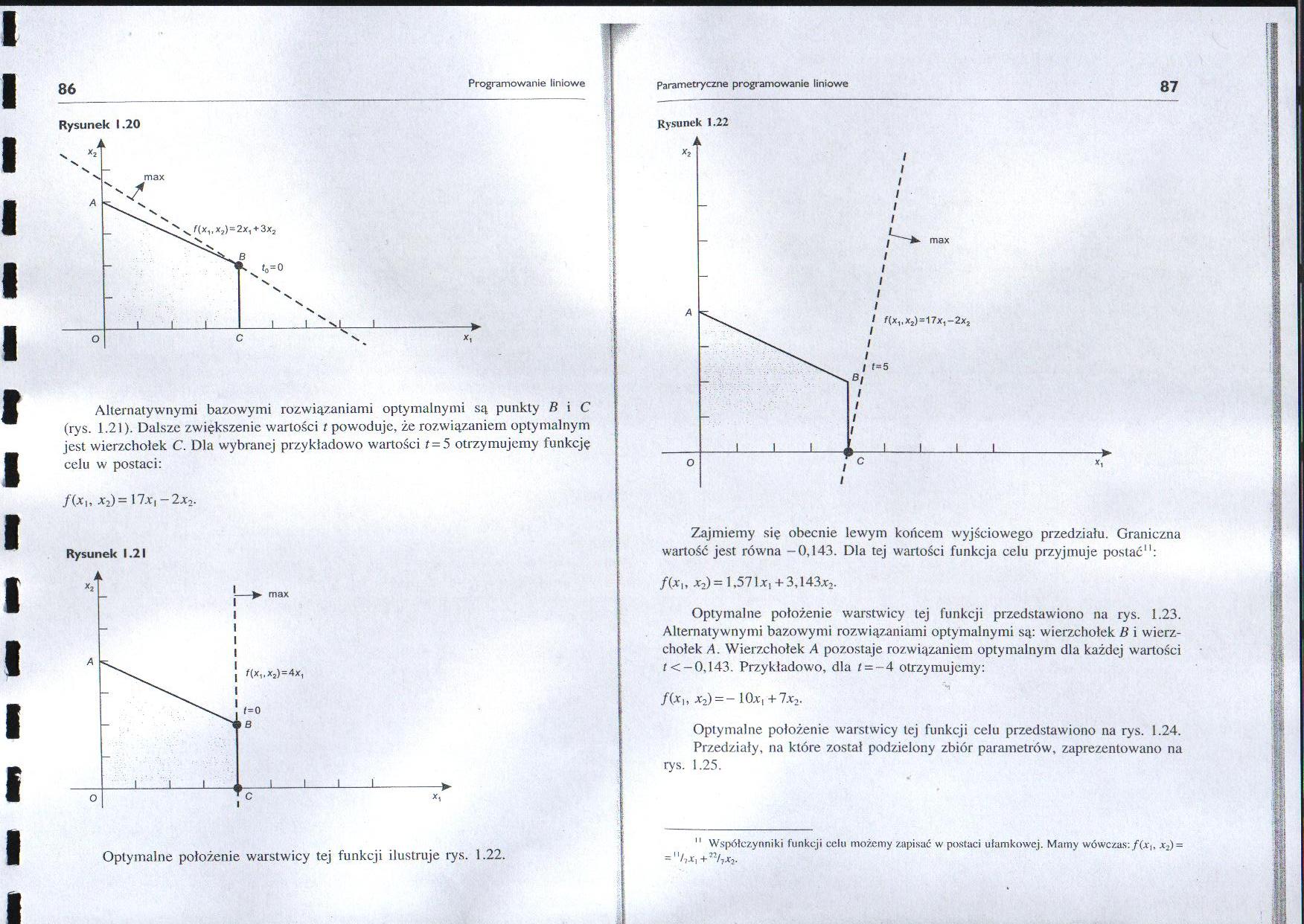
Rysunek 1.20

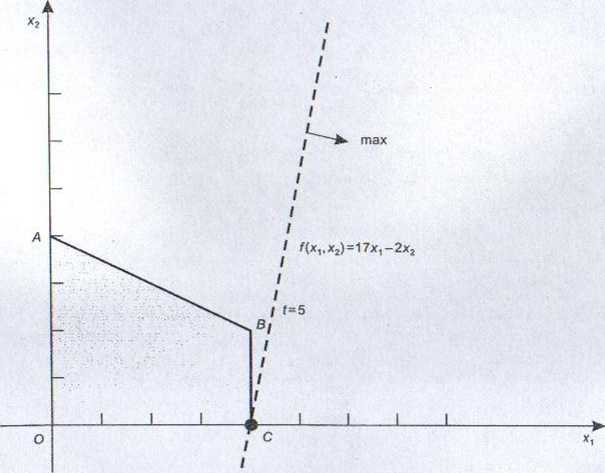
Alternatywnymi bazowymi rozwiązaniami optymalnymi są punkty B i C (rys. 1.21). Dalsze zwiększenie wartości t powoduje, że rozwiązaniem optymalnym jest wierzchołek C. Dla wybranej przykładowo wartości t= 5 otrzymujemy funkcję celu w postaci:

f(xi, jc₂)= 17xi -2x₂.

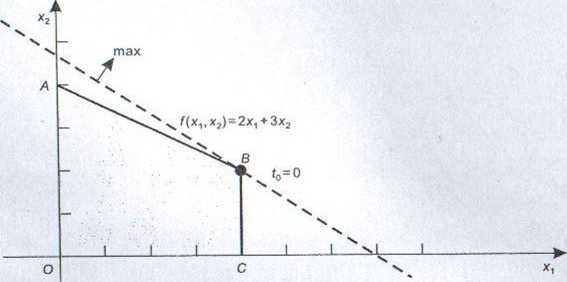
Rysunek 1.21

Optvmalne położenie warstwicy tej funkcji ilustruje rys. 1.22.

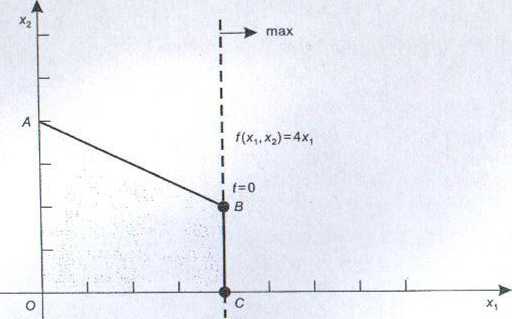
Rysunek 1.22

Zajmiemy się obecnie lewym końcem wyjściowego przedziału. Graniczna wartość jest równa -0,143. Dla tej wartości funkcja celu przyjmuje postać":

f(x\, x₂) = 1.571 cc, + 3,143*2-

Optymalne położenie warstwicy tej funkcji przedstawiono na rys. 1.23. Alternatywnymi bazowymi rozwiązaniami optymalnymi są: wierzchołek B i wierzchołek A. Wierzchołek A pozostaje rozwiązaniem optymalnym dla każdej wartości t <-0,143. Przykładowo, dla l=-4 otrzymujemy:

%

f(x„ x₂) = - IOjc, +7.r₂.

Optymalne położenie warstwicy tej funkcji celu przedstawiono na rys. 1.24. Przedziały, na które został podzielony zbiór parametrów, zaprezentowano na rys. 1.25.

" Współczynniki funkcji cc!n możemy zapisać w postaci ułamkowej. Mamy wówczas:/O,, jc₂) = = "A,*, +^,2I₇x₂.