028 029 2

28 Programowanie liniowe

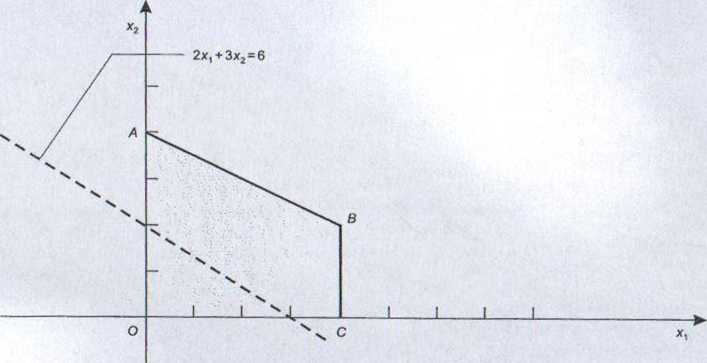
Rysunek 1.7

Rysunek 1.8

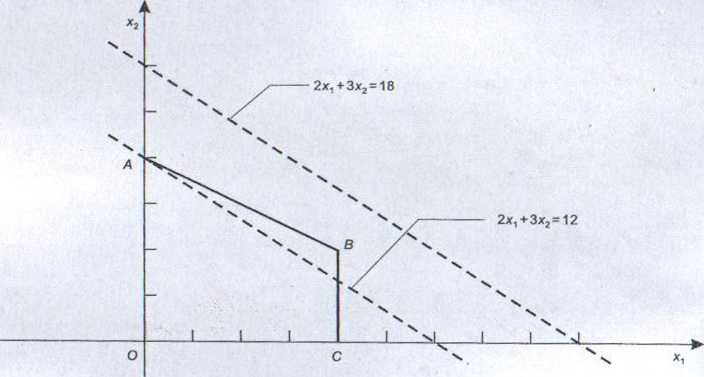
punkty tej prostej ze zbiorem rozwiązań dopuszczalnych (rys. 1.8), czyli istnieje możliwość poprawy rozwiązania. Otrzymana prosta jest równoległa do prostej rozpatrywanej poprzednio. Widzimy więc, że przesuwając warstwicę funkcji celu coraz wyżej, polepszamy wartość funkcji celu. Kontynuując poszukiwanie wartości optymalnej funkcji celu, wybieramy wartość zysku równą 18.

Rysunek 1.9

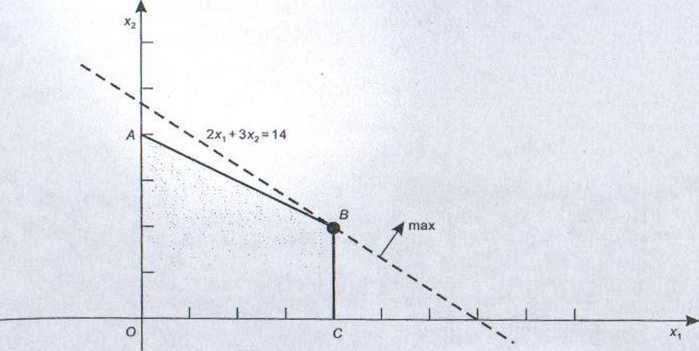
Rysując prostą 2x, +3x₂= 18, stwierdzamy, że nie istnieją punkty wspólne tej prostej ze zbiorem rozwiązań dopuszczalnych (rys. 1.8) nie istnieje więc taki plan produkcji, który dawałby zysk równy 18. Przesunęliśmy się więc zbyt daleko. Pamiętajmy, że interesuje nas takie rozwiązanie, które byłoby jednocześnie dopuszczalne, a z drugiej strony położone „najwyżej”. Takim rozwiązaniem jest punkt wierzchołkowy B (rys. 1.9). Na rysunku tym zaznaczono również warstwicę przechodzącą przez rozwiązanie optymalne oraz kierunek i zwrot wektora wskazującego na optymalne przemieszczenie warstwicy funkcji celu.

Wierzchołek B stanowi przecięcie prostych a, +2.r₂ = 8 oraz 4x_t = 16. Rozwiązując ten układ warunków, stwierdzamy, ze a, = 4 i x₂ = 2, stąd wartość funkcji celu w tym wierzchołku wynosi 14.

W rozpatrywanym przez nas zadaniu rozwiązaniem optymalnym był wierzchołek zbioru rozwiązań dopuszczalnych. Występuje to zawsze wtedy, kiedy istnieje dokładnie jedno rozwiązanie optymalne. W przypadku większej liczby rozwiązań optymalnych (sytuacja taka, jak zobaczymy dalej, również jest możliwa) przynajmniej jedno z nich jest rozwiązaniem wierzchołkowym.

1.2.4. Gradient funkcji celu

Zamiast stosować metodę prób i błędów do wyznaczenia optymalnego przemieszczenia warstwicy funkcji celu, wykorzystamy pojęcie gradientu. Funkcja f(xi, a₂) ma pochodne cząstkowe równe odpowiednio:

£-2.    f-3.

OT,    8x₂