108 109 2

108 Programowanie liniowe całkowitoliczbowe

Rysunek 2.1

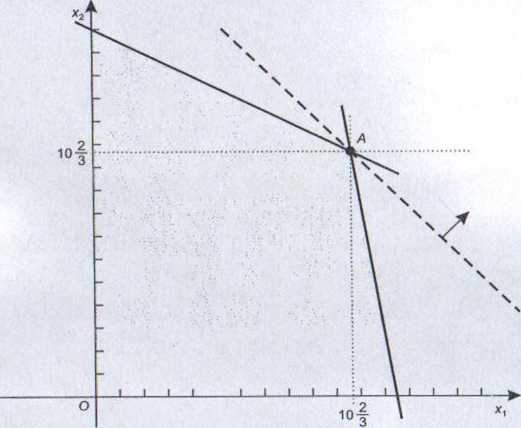
Rozpatrzymy najpierw możliwość podziału ze względu na zmienną x₍, która w otrzymanym przez nas rozwiązaniu przyjęła wartość równą 10~/₃. W rozwiązaniu dopuszczalny m całkowitoliczbowym wartość ta będzie mniejsza od 10 lub większa

od 11 (rys. 2.2).

Można więc dotychczasowy obszar dopuszczalny podzielić na dwie części: pierwszą, w której do dotychczasowych warunków określających zbiór dopuszczalny dołączymy dodatkowy warunek 0=Sx, < 10 oraz drugi, w którym dodatkowo będziemy mieli x, > 11. Dzieląc w taki sposób wyjściowy obszar na dwie części i pomijając te wszystkie punkty, dla których 10 < x, < 11, nie utraciliśmy żadnego z interesujących nas punktów obszaru dopuszczalnego zadania wyjściowego, uwzględniającego warunki całkowitoliczbowości. Pełna postać otrzymanych zadań jest następująca:

Zadanie 2

x, +x₂ —'■> max, x, + 2x₂ < 32,

18.t| + 3x₂ < 224,

0«£x,    10,

x₂^0,

x_h x₂ — całkowite.

Zadanie 3

jc, +*2 —» max, jc, + 2*2 <132,

18x, + 3r_? ^ 224,

*i > 11,

*1, a:₂ > 0,

x,, x₂ — całkowite.

Rysunek 2.2

10

♦

11

Dokonany podział zbioru rozwiązań dopuszczalnych zrelaksowanego zadania I na dwie części względem jc, oraz rozwiązanie zadań 2 i 3 metodą geometryczną pokazano na rysunku 2.3.

Rysunek 2.3

o

X.

Rozwiązaniem optymalnym zadania 2 jest punkt #(10, 11). Wartość funkcji celu w tym punkcie wynosi 21. Rozwiązaniem optymalnym zadania 3 jest punkt C(ll. 8²/j), a wartość funkcji celu w tym punkcie wynosi 19²/,. Rozwiązanie zadania 2 jest całkowitoliczbowe, natomiast rozwiązanie zadania 3 nie ma tej własności. Zadanie 2 można więc zgodnie z przyjętą uprzednio zasadą podzielić na kolejne zadania i szukać ich rozwiązań.

Czy jest to jednak potrzebne? Wartość rozwiązania optymalnego zadania 2, wynosząca 21, jest ograniczeniem nałożonym na wartość rozwiązania optymalnego wyjściowego problemu. Dokonując podziału zadania 3, nie otrzymamy rozwiązania, które dałoby wartość funkcji celu lepszą od 197_v Dalszy podział obszaru II nie