024 025 2

24 Programowanie liniowe

1.2.2. Zbiór rozwiązań dopuszczalnych

W zadaniu rozpatrywanym w przykładzie 1.1 mamy dwie zmienne decyzyjne, dlatego też możemy je rozwiązać metodą geometryczną. Zauważmy, że każdemu planowi produkcji (*,, x₂) na płaszczyźnie Ox_tx₂ przyporządkowany jest w sposób jednoznaczny punkt P o współrzędnych jc, oraz x₂, który zapisujemy jako P(x_{, x₂). 1 na odwrót, każdemu punktowi P(x_u x₂) płaszczyzny Ox_tx₂ odpowiada pewien plan produkcji. Tak więc w dalszych rozważaniach będziemy utożsamiali plany produkcji z punktami płaszczyzny.

Zaczniemy od geometrycznego wyznaczenia dopuszczalnych planów produkcji. Rozwiązanie problemu optymalizacyjnego nazwiemy rozwiązaniem dopuszczalnym, jeżeli spełnia ono wszystkie warunki ograniczające występujące w rozpatrywanym problemie. Tak więc, aby znaleźć zbiór wszystkich dopuszczalnych planów produkcji dla zadania z przykładu 1.1, należałoby znaleźć kolejno zbiory punktów płaszczyzny, spełniające warunki ograniczające (1.1)—(1.3) oraz warunki nieujcmności (1.4) i (1.5). Ponieważ zbiór rozwiązań dopuszczalnych zawiera jedynie takie rozwiązania, które jednocześnie spełniają wszystkie warunki ograniczające, w dalszej kolejności wyznaczamy część wspólną znalezionych uprzednio zbiorów.

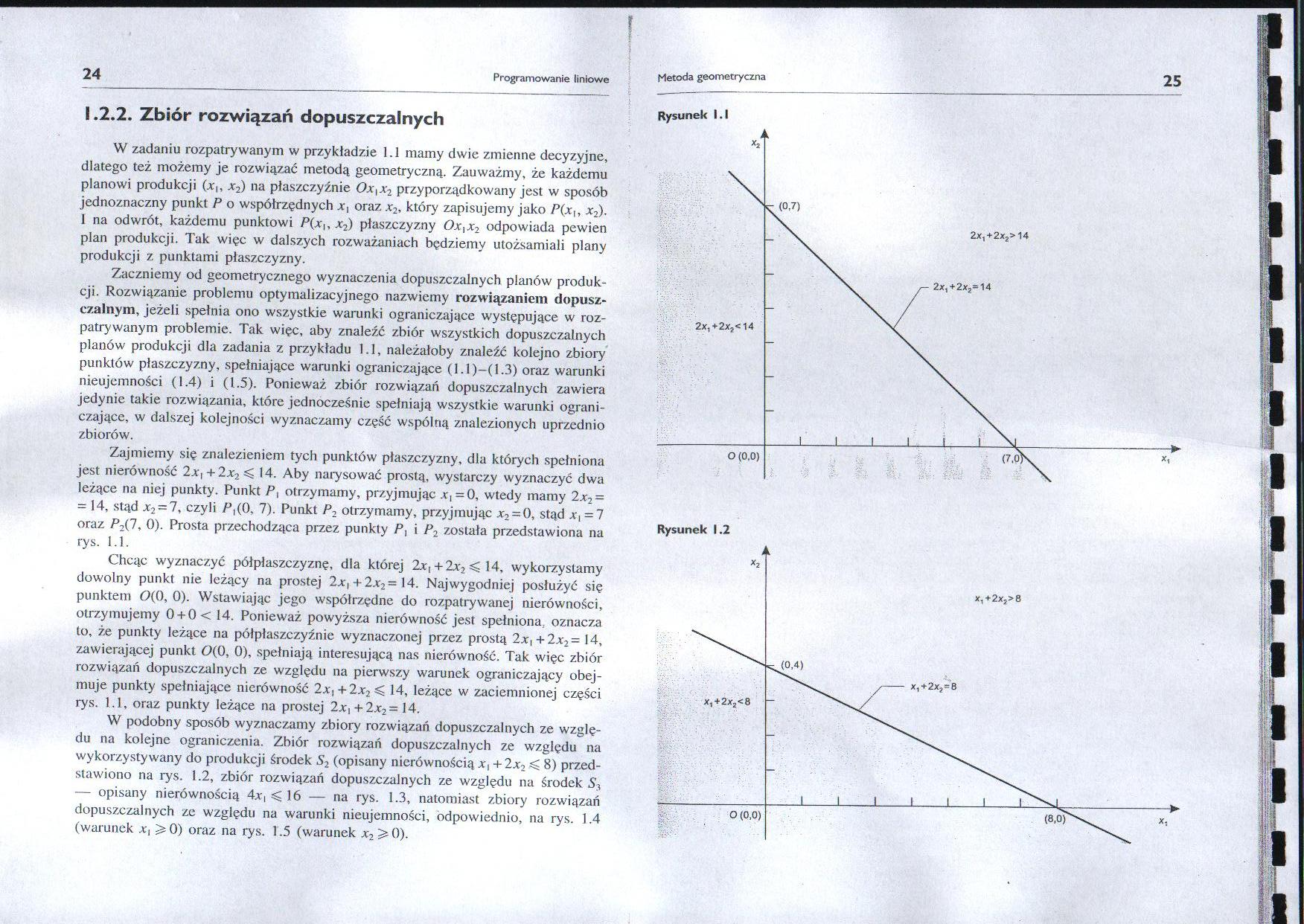
Zajmiemy się znalezieniem tych punktów płaszczyzny, dla których spełniona jest nierówność 2*| + 2x₂< 14. Aby narysować prostą, wystarczy wyznaczyć dwa leżące na niej punkty. Punkt P, otrzymamy, przyjmując x, =0, wtedy mamy 2x₂-

-    14, stąd *2 = 7, czyli /^J,(0. 7). Punkt P₂ otrzymamy, przyjmując x₂ = 0, stąd *, = 7 oraz P₂(7, 0). Prosta przechodząca przez punkty P, i P₂ została przedstawiona na rys. 1.1.

Chcąc wyznaczyć półpłaszczyznę, dla której 2x, +2x₂ < 14, wykorzystamy dowolny punkt nie leżący na prostej 2x_[ + 2x₂= 14. Najwygodniej posłużyć się punktem 0(0, 0). Wstawiając jego współrzędne do rozpatrywanej nierówności, otrzymujemy 0 + 0 < 14. Ponieważ powyższa nierówność jest spełniona oznacza to, że punkty leżące na półpłaszczyźnie wyznaczonej przez prostą 2x,+2x₂- 14, zawierającej punkt 0(0, 0), spełniają interesującą nas nierówność. Tak więc zbiór rozwiązań dopuszczalnych ze względu na pierwszy warunek ograniczający obejmuje punkty spełniające nierówność 2x,+2x₂< 14, leżące w zaciemnionej części rys. 1.1, oraz punkty leżące na prostej 2x,+2x₂ = 14.

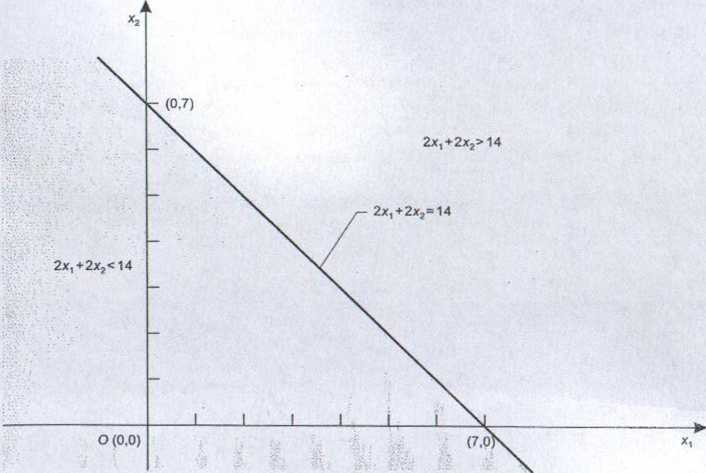
W podobny sposób wyznaczamy zbiory rozwiązań dopuszczalnych ze względu na kolejne ograniczenia. Zbiór rozwiązań dopuszczalnych ze względu na wykorzystywany do produkcji środek S₂ (opisany nierównością x, + 2x₂ < 8) przedstawiono na rys. 1.2, zbiór rozwiązań dopuszczalnych ze względu na środek 5,

—    opisany nierównością 4x, <16 — na rys. 1.3, natomiast zbiory rozwiązań dopuszczalnych ze względu na warunki nieujemności, odpowiednio, na rys. 1.4 (warunek x, > 0) oraz na rys. 1.5 (warunek x₂ > 0).

Metoda geometryczna

25

Rysunek l.l

Rysunek 1.2