212 213

Metody wielokryterialne

212

Zbiór rozwiązań dopuszczalnych tego zadania jest jednoelcmentowy. Jedynym rozwiązaniem dopuszczalnym jest punkt B. Jest on oczywiście również rozwiązaniem optymalnym lego zadania.

Powyższy przykład ilustruje często występującą możliwość redukcji zbioru rozwiązań dopuszczalnych do zbioru jednoelementowego. Jeżeli wystąpi taka sytuacja, to kryteria rozpatrywane w kolejnych etapach postępowania sekwencyjnego nie mają żadnego wpływu na wybór rozwiązania końcowego. Skłania to do przyjęcia możliwości wykorzystania quasi-hierarchii.

W zmodyfikowanym sposobie postępowania do kolejnego etapu przechodzą te rozwiązania, które są optymalne dla rozpatrywanego aktualnie kryterium, oraz dodatkowo te, dla których wartość rozpatrywanego kryterium jest nieco mniejsza od optymalnej, lecz różnica między tymi wartościami mieści się w przedziale tolerancji zadanym przez decydenta. Zaletą lego postępowania jest zagwarantowanie możliwości rzeczywistego wpływu wszystkich kryteriów na wybór rozwiązania końcowego, a jego wadą — możliwość zaistnienia sytuacji, w której otrzymane rozwiązanie nie będzie sprawne.

Przykład 4.8

Przyjmiemy taką samą hierarchię kryteriów jak w przykładzie 4.7. W drugim etapie do wyboru decyzji optymalnej ze względu na drugie kryterium wykorzystamy rozwiązania, dla których pierwsze kryterium przyjmuje wartość optymalną,

Rysunek 4.1 I A

*2

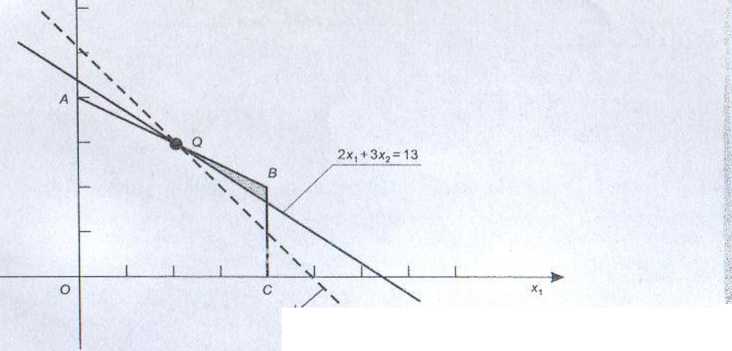
oraz te, dla których różnica między wartością optymalną dla tego kryterium a wartością w rozpatrywanym rozwiązaniu jest nic większa niż 1.

W pierwszym etapie rozwiązujemy takie samo zadanie jak w przykładzie 4.7. Optymalna wartość funkcji celu wynosi 14. Zadanie dla drugiego etapu procedury quasi-hierarchicznej ma postać:

-2x_{ -2x₂ —» max,

jti +2*2 ^ 8.

4x_t    16,

2x_t + 2ix₂3* 13, x„ x₂^0.

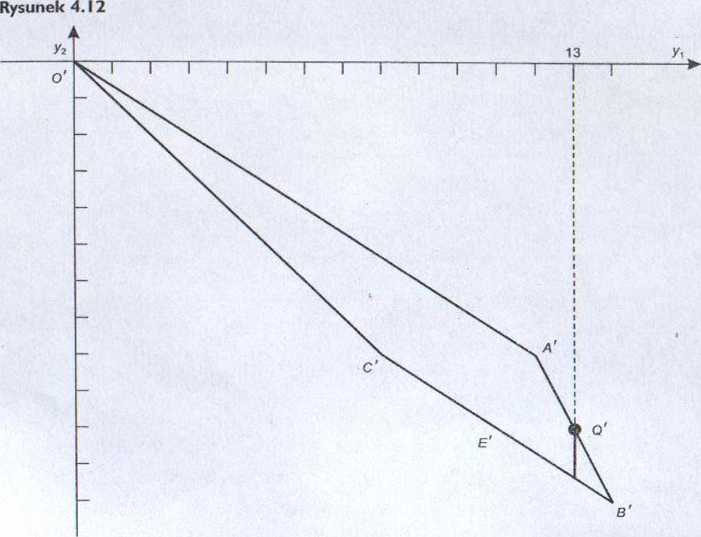
Rozwiązanie tego zadania w przestrzeni decyzyjnej oraz kryterialnej ilustrują, odpowiednio, rys. 4.II i 4.12.

Widzimy, że punkt Q' jest rozwiązaniem niezdominowanym w przestrzeni kryterialnej, stąd odpowiadający mu punkt Q w przestrzeni decyzyjnej jest rozwiązaniem sprawnym.