110 111

I 10

Programowanie liniowe całkowito!iczbowe

jest celowy, gdyż nie jest możliwe wygenerowanie rozwiązania całkowitolicz-bowego lepszego niż to, które otrzymaliśmy, rozwiązując zadanie 2. Tak więc punkt B(10, 11) jest rozwiązaniem optymalnym wyjściowego zadania, opisanego w przykładzie 2.1.

Rozpatrzymy obecnie możliwość podziału zadania 1 ze względu na zmienną x₂. Przypomnijmy, że dysponujemy rozwiązaniem, którego współrzędne wynoszą A(10%, 10²/j). Zmienna *₂ w optymalnym rozwiązaniu całkowitoliczbowym również nic może przyjąć wartości 10²/₃. Wartość ta będzie mniejsza lub równa 10 albo też większa lub równa 11 (rys. 2.4).

Rysunek 2.4

10

*2

>

Tym razem zbiór rozwiązań dopuszczalnych zrelaksowanego zadania 1 podzielimy na następujące części: pierwszą, w której dołączymy dodatkowy warunek 0 < x₂ < 10, oraz drugą, w której będziemy mieli x₂ > 11. W ten sposób otrzymamy następujące problemy:

Zadanie 2'    Zadanie 3'

x, + x₂ —» max, *, + 2x₂ < 32, 18;t|+3jc₂ < 224,

0<*₂< 10,

A|, *2 > 0,

*,, *2 — całkowite.

je, + *₂ —> max, *, +2*2 < 32, 18*,+3*2 <224,

*,, *₂ > 0,

x„ *2 — całkowite.

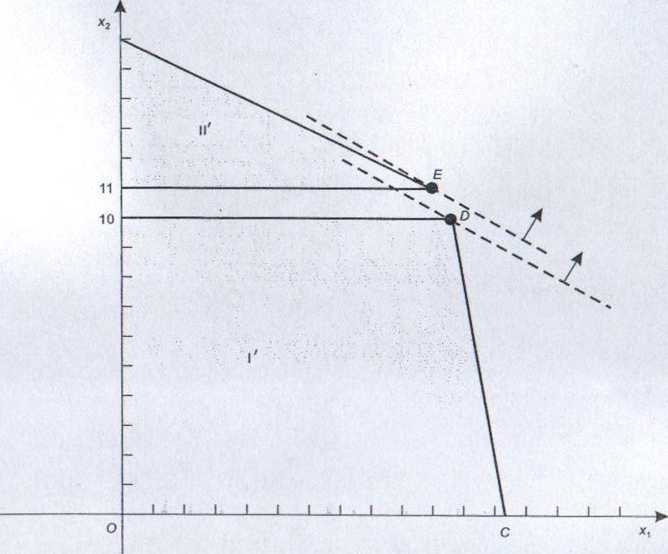
Dokonany podział zbioru rozwiązań dopuszczalnych zrelaksowanego zadania 1 na dwie części względem *₂ oraz rozwiązania zadań 2' i 3' metodą geometryczną pokazano na rysunku 2.5.

Rozwiązaniem optymalnym zadania 2' jest punkt £>(10%, 10), a optymalna wartość funkcji celu wynosi 20%. Rozwiązaniem optymalnym zadania 3' jest punkt E(10, 11), a optymalna wartość funkcji celu jest równa 21. Ponieważ rozwiązanie zadania 3' jest całkowitoliczbowe i na dodatek jest lepsze od rozwiązania niecałkowitoliczbowego zadania 2', dalszy podział zadania 2', choć możliwy, nie jest potrzebny.

-V ■    ■ .    .    ■__-_    ■    y

Rysunek 2.5

2.2.2. Zadanie mieszane

Przypomnijmy, że mieszanymi zadaniami programowania liniowego w licz-, bach całkowitych są takie zadania, w których warunek całkowitoliczbowości nałożony jest na niektóre zmienne decyzyjne, natomiast pozostałe mogą przyjmować dowolne wartości. Powróćmy na chwilę do zadania z przykładu 2.1. Jeżeli założymy, że zmienna x, ma być całkowita, a zmienna jc₂ może przyjmować dowolne wartości, to otrzymamy zadanie mieszane. Zbiór rozwiązań dopuszczalnych takiego zadania ilustruje rys. 2.6. Przykład innego zadania mieszanego otrzymamy wówczas, gdy założymy, że zmienna jc₂ w przykładzie 2.1 ma być całkowita, a zmienna x, może przyjmować dowolne wartości (rys. 2.7).

Zaletą naszkicowanej uprzednio metody podziału i ograniczeń jest to, że możliwe jest również jej wykorzystanie w przypadku zadań mieszanych. Prześledzimy tę możliwość, rozwiązując następne zadanie (przykład 2.2). W kolejnych iteracjach trzeba będzie znaleźć rozwiązanie kilku pomocniczych zadań programowania liniowego.