33932 Rysunek 202

240

I/V ... B. Kinematyka

prędkość średnia punktu na drodze s₂ — s i = = As wyniesie

c. Przyspieszenie w ruchu zmiennym po linii prostej

s₂ —    As

®śr ~    ⁼⁼    .

i₂ — ti    At

[33]

Jeżeli natomiast będziemy rozpatrywać coraz krótsze przedziały czasu At zbliżając się w granicy do zera, to prędkość średnia zbliżać się będzie do pewnej gfanicy, którą nazywamy prędkością punktu w chwili t

As    di

v = lim -= —    [34]

At-*0 At    dż

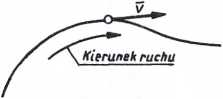
A zatem prędkość w chwili t jest pochodną drogi względem czasu. Wynika z tego wniosek, że prędkość określona wektorowo w danej chwili jest zawsze styczna do toru i skierowana w kierunku ruchu punktu (rys. 55).

Rys. 55

Jeżeli ruch punktu jest określony równaniami parametrycznymi [29], to rzuty prędkości na osie prostokątnego układu współrzędnych są określone przez pochodne odpowiednich współrzędnych względem czasu

v_x =

óx

~&t’

Vy

dy

~dt'

v_z

d z d t

[35]

a prędkość punktu (rys. 56) v = V^vl+^vy    t³^]

Prędkość ruchu punktu w płaszczyźnie xy jest określona wzorem

v = ]/ v_x+v²y    [37]

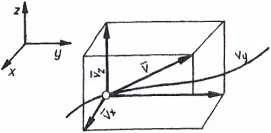
Rys. 56

Jeżeli torem punktu jest linia prosta, to wektor prędkości tego punktu jest zawsze skierowany wzdłuż tej prostej. Zwrot wektora prędkości jest zgodny z kierunkiem ruchu. Jeżeli w chwili t! punkt miał prędkość v_lt zaś w chwili t₂ swą prędkość zwiększył do v₂ (rys. 57), to średnie przyspieszenie punktu wyniesie

v₂ — vi Av t₂-ti At

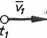
Rys. 57

[38]

_m m t₂    Kierunek

ruchu

Średnie przyspieszenie jest więc równe przyrostowi prędkości punktu odniesionemu do jednostki czasu.

Jeżeli przedział czasu At będzie się zbliżać w granicy do zera, to przyśpieszenie średnie zbliża się do granicy, którą nazywamy przyśpieszeniem chwilowym punktu w chwili t Av    dv

a = lim -=- [39]

At-*o At    dt

A zatem przyśpieszenie w chwili t w ruchu punktu po linii prostej jest równe pochodnej prędkości względem czasu.

Jednostką podstawową przyśpieszenia jest 1 m/s², jednostkami pochodnymi 1 km/h², 1 m/min² itp. Podobnie jak prędkość, przyśpieszenie jest wielkością wektorową.

d. Przyspieszenie w ruchu po linii krzywej

Rozpatrzmy dowolny ruch punktu po dowolnej krzywej. Załóżmy, że w chwili ti punkt znajdował się w położeniu

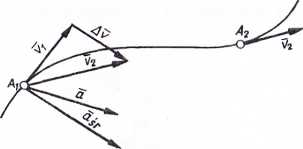
Rys. 58

2. Prędkość i przyspieszenie punktu

241

Ai_t zaś w chwili t₂ w położeniu A% (rys. 58), przy czym t₂ — t_t = At. Kierunki wektora prędkości punktu zawsze są skierowane zgodnie z kierunkiem stycznej do toru w danym punkcie. Jeżeli do punktu A_x przeniesiemy wektor vi ² punktu A_2t to wektor łączący koniec wektora vi z końcem wektora v₂ będzie przedstawiać przyrost wektora prędkości Av między położeniami A_± i A₂ (w czasie At). Kierunek wektora Av ma również wektor średniego przyśpieszenia dśr» przy czym

Av

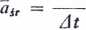
Jeżeli At będzie dążyć do zera, to granicę, do której będzie dążyć średnie przyśpieszenie, nazwiemy przyśpieszeniem a w danej chwili t

Av    dv

a = lim (a_ir) = lim —— =- [40]

f_*0    /-*<) At    dt

Zależność [40] różni się tym od zależności [39], że występuje tu pochodna wektorowa prędkości względem czasu. Wektor przyśpieszenia a znajduje się w płaszczyźnie promienia krzywizny toru w danym punkcie.

Jeżeli zgodnie z [29] tor punktu można przedstawić w postaci równań parametrycznych ruchu, to miary rzutów przyśpieszenia a na osie współrzędnych wyniosą

d²x    d²y    d²z

a x —— , a y — , d t^2 y At^1	^az - . 2 dt^2
	[41]
zaś przyśpieszenie
a = ]/a^2+a^2-{-a^2	[42]

W przypadku ruchu punktu po dowolnej krzywej płaskiej (w płaszczyźnie xy) wystąpią oczywiście tylko dwie składowe przyśpieszenia a_x i a_y.

e. Przyśpieszenie styczne i normalne

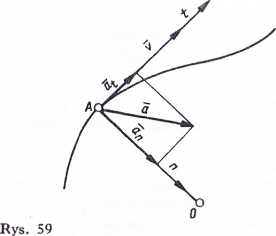
Przyśpieszenie a dowolnego punktu A poruszającego się po dowolnej krzywej można rozłożyć na dwie składowe: przyśpieszenie styczne a_t i przyśpieszenie normalne a_n (rys. 59).

Przyśpieszenie styczne, mające kierunek prędkości punktu, jest równe pochodnej prędkości względem czasu

dv

«,=-    [43]

Przyśpieszenie styczne charakteryzuje liczbową zmianę prędkości i jest skierowane zgodnie z kierunkiem ruchu lub odwrotnie w zależności od tego, czy prędkość wzrasta czy maleje.

Przyśpieszenie normalne określa się zależnością

v²

<*n = -- [44]

Q

gdzie v — prędkość chwilowa punktu, q — promień krzywizny w danym punkcie toru (e — O A na rys. 59).

Przyśpieszenie normalne jest skierowane zawsze do środka krzywizny, stąd jego druga nazwa — przyśpieszenie dośrodkowe.

Za pomocą wzorów [43] i [44] można wyznaczyć przyśpieszenie całkowite

¹⁴⁵¹

Kierunek wektora przyśpieszenia wyznaczają wartości kątów, jakie wektor przyśpieszenia tworzy z kierunkiem stycznej i normalnej (rys. 59).

_    a_t    _    a„

cos (a, t) = —; cos(a, n) = — a    a

f. Przypadki szczególne ruchu punktu

1) Ruch jednostajnie zmienny. Ruchem jednostajnie zmiennym nazywamy ruch, w którym prędkość zmienia się o jedna-