50818 str281

§ 3. TENSORY W PRZESTRZENI RIEMANNA 281

\

Definicja 2. Formą metryczną lub formą fundamentalną danej przestrzeni nazywamy wyrażenie

(3.4)    a_mndx^mdx\

Definicja 3. Kwadratem elementu liniowego nazywamy ds².

Definicja 4. Przestrzenią Riemanna nazywamy przestrzeń, w której został określony metryczny kowariantny tensor a_mn rzędu drugiego będący tensorem symetrycznym.

Własność 2. W przestrzeni Riemanna jest określona forma metryczna (3.4) i jest ona równa kwadratowi elementu liniowego ds¹, pomnożonemu przez e, gdzie s = 1 lub e = — 1, tak ażeby

(3.5)    ds² = Ea_mndx^mdxⁿ^0.

Definicja 5. Dopełnieniem algebraicznym A^mn elementu a_m„ nazywamy wartość pod-wyznacznika uzyskanego z wyznacznika \a_mn\ po skreśleniu w-tego wiersza i n-tej kolumny pomnożoną przez (—l)^m+".

Dopełnienie algebraiczne elementu a_m„ nazywane jest również podwyznacznikiem względnym wyznacznika |a_m„| związanym z elementem a_m„.

Własność 3. Zbiór dopełnień algebraicznych A^mn elementów tensora fundamentalnego a_mn jest tensorem kontruwariantnym rzędu drugiego.

Własność 4. Jeżeli a = \a_mn\ i A^m" jest dopełnieniem algebraicznym elementu a_m„, to zachodzi następujący związek:

(3.6)    a_mrA^ms = a_rmA^sm = ó’a , gdzie <5* jest deltą Kroneckera.

Definicja 6. Tensorem metrycznym kontrawariantnym lub sprzężonym z tensorem fundamentalnym przestrzeni nazywamy tensor

„mn

a

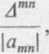
(3.7)

gdzie A^mn jest dopełnieniem algebraicznym elementu a_m„.

Własność 5. Tensor metryczny kontrawariantny jest tensorem symetrycznym. Własność 6. Jeżeli a_mn jest tensorem fundamentalnym i a_mn = 0 dla m j=n oraz a_m„ ^ 0 dla m = n, to tensor sprzężony

0	dla m n,
1	dla m = n .
	\

(3.8)

Własność 7. Jeżeli / są współrzędnymi w ortogonalnym układzie kartezjańskim oraz x^r są współrzędnymi w dowolnym układzie krzywoliniowym, przy czym / = /(x^l, x²,..., x^N)„ to tensor metryczny a_m„ przestrzeni związanej z układem x^r określony jest wzorem

(3.9)

Edf dy^k