55825 skan0013 (4)

SD w równaniu (2.3.1) jest stała, tzn. gdy g(x) = p, a ponadto funkcja / występują! w tym równaniu jest:

(i)    bądź to wielomianem stopnia n,

(ii)    bądź sumą o postaci a sin kx + (3 cos kx,

(iii)    bądź funkcją typu ae^bx, gdzie b —p,

(iv)    bądź też sumą lub iloczynem funkcji podanych w punktach (i)—(iii), W każdym z wymienionych wyżej przypadków całkę szczególną przewiduj enj

w tej samej postaci co funkcja /, np. gdy

f(x) = 2 sin 5x — cos 5#,

to całkę szczególną przewidujemy w postaci

Y(x) = a sin 5x + b cos 5x.,

Stałe a i b należy tak wyznaczyć, aby funkcja Y spełniała równanie (2.3.1).

Podkreślmy, że metodę uzmiennienia stałej możemy zawsze stosować, jednaki w porównaniu z metodą przewidywań jest to metoda, która może dostarczyć nhi kłopotów związanych z liczeniem całki. Stąd praktyczna rada, aby stosować metól przewidywań w tych przypadkach, gdy jest to możliwe.

Wyznaczyć całki ogólne podanych niżej równań różniczkowych:

3. y' + 2y = 2x³

4. y' + y = sin 2x + e^5x

Rozwiązania

1. Wyznaczmy najpierw całkę ogólną równania jednorodnego, tzn. równania:

y' + yctgz = 0.

Po rozdzieleniu zmiennych

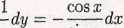
y    sina:

sina;

i po scałkowaniu mamy

In |y| = — ln j sin x\ 4- ln jłŚj

Stąd funkcja

yo(x) -

C

sin x

jest całką ogólną równania jednorodnego.

3;l

! kilkę    równania niejednorodnego wyznaczymy metodą uzmiennienia

filiiln.l, gdyż metody przewidywań nie można zastosować do naszego zadania. W lvm celu w wyrażeniu na yo zastąpmy stałą C przez nieznaną funkcję L, a następnie funkcję L wyznaczymy tak, aby wyrażenie

sin a;

liyln rozwiązaniem równania niejednorodnego postaci:

Y'(x) 4- Y(x)ctgx =    (2.3.5)

■ cos² x

W tym celu obliczmy Y\ korzystając ze wzoru na pochodną ilorazu, więc

llS Sin®0.L(®) cos,a:

W    . 2    ■

sm x

Po wstawieniu do równania (2.3.5) mamy

L'(x) sin x — L(x) cos a:    L(x)    1

SflJR-. ₂    -+ -r^ctg® = —o—

siu x    I sin a:    cos² ®

. sin® mm = —2 >

cos² x

J

L{x)

■dx.

I po uporządkowaniu I stąd Podstawmy

cos x = t, więc sin xdx = dt.

/godnie z twierdzeniem o całkowaniu przez podstawienie mamy

m=- /RH+K=—+■

J t² t    cos®

W ostatnim wyrażeniu na L przyjmiemy stałą Ci = 0, gdyż zgodnie z metodą fłimionnlenia stałej wystarczy wyznaczyć dowolną funkcję L o podanych wyżej własnościach. Stąd funkcja

MBE

i

sm x cos x

JflSl. szukaną całką szczególną równania niejednorodnego.

Z powyższego wynika, że szukana całka ogólna ma postać:

lin x coi w

2lito) ■ MW