59961 skrypt022

nu

Kozdziat d. Froces próbkowania

2    2 _e)nv_ar/2 _ _e-jno>_sr/2

T_s nuj_s/2    2j

JL__1

T_s nuj_s/2

s'n\(nu!_sr/2).

Na podstawie zależności (3.1) i (3.2) sygnał spróbkowany możemy wyrazić wzorem

OO

x\t) = x(t) J2 c_ne^jnu,J<,    (3.4)

n=-oo

Interpretacja procesu próbkowania jako procesu modulacji nasuwa przypuszczenie, że w wyniku próbkowania powstają nowe składowe w widmie sygnału (produkty modulacji). Aby zbadać to zjawisko, załóżmy, że sygnał ciągły x(t) ma skończoną energię. Sygnał spróbkowany x\t) ma wówczas także skończoną energię. Zatem

(3.5)

(3.6)

X“(jw) = JF{z#(<)} = [°°    .

^ ^J    J — OO

Ze wzorów (3.2) i (3.5) otrzymujemy wyrażenie

roo    / °°    \

X

'(jw) = / x(i) ( X] c_ne^ e-^df,

\n=—oo    /

które po zamianie kolejności całkowania i sumowania przyjmuje postać

x'Q

OJ)

^w    roo

J2 ^Cn /

_ J-oo

-j (w-nw₃)tĄi

lub ostatecznie

OO

^“(jw) = J2 ^c”-^x (j(^w - ^nw.o) •

72 — — OO

(3.7)

(3.8)

Na podstawie wzoru (3.8) możemy sformułować wniosek:

Widmo sygnału spróbkowanego powstaje z wid na sygnału ciągłego przez sumowanie (z wagami równymi współczynnikom szeregu Fouriera funkcji przełączającej) translacji tego widma w odstępach równych częstości próbkowania.

Przykład

Rozważmy sygnał ciągły x(t) o przebiegu

x(t) =

27T

(sin(cu_gt/2)\

V <V/2 )

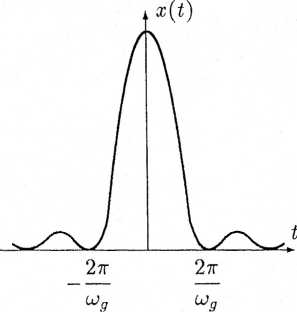
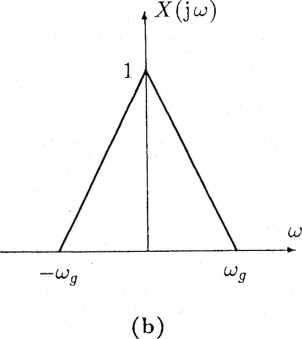
Rys. 3.4. Sygnał przykładowy: (a) przebieg sygnału x(t), (b) widmo Jć(jw) przedstawionym na rys. 3.4a. Widmo amplitudowe |X(jw)| tego sygnału ma kształt trójkątny (rys. 3.4b). Widmo fazowe jest zaś równe zeru, a zatem |X(jw)| = X(jw). Sygnał x(t) jest nieograniczony w czasie, jako że jego widmo leży w przedziale ograniczonym¹.

Sygnał x(t) poddajemy próbkowaniu za pomocą funkcji przełączającej o przebiegu pokazanym na rys. 3.5a. W ten sposób powstaje sygnał spróbkowany x^{t) przedstawiony na rys. 3.6. Widmo sygnału a^(f) otrzymujemy na podstawie wzoru (3.8). Składowe widma przesunięte o nu)_s są pomnożone odpowiednio przez współczynniki c_n (rys. 3.5b). Na rysunku 3.7 pokazano widmo sygnału x\t) przy założeniu, że częstość próbkowania u_s jest co najmniej dwa razy większa niż podwojona największa pulsacja sygnału x(i) — w naszym przykładzie równa u>_g. W tym przypadku możemy odtworzyć widmo X(ju>) sygnału ciągłego (a tym samym i sygnał x(t)) na podstawie widma X^(]u). W tym celu należy zastosować filtr dolnoprzepustowy, który usunie wszystkie przesunięte składowe widma. Jeśli zmniejszymy częstość próbkowania u>_s, to poszczególne składowe w widmie sygnału mogą się na siebie częściowo nasunąć (rys. 3.8). Wówczas nie będzie już można odtworzyć sygnału x(t) na podstawie sygnału    Ten efekt nazywamy

aliasingiem².    I

1

Jest to ogólna właściwość sygnałów. Sygnały o ograniczonym czasie trwania mają zaś widmo o nieskończonej rozciągłości.

2

Ściśle; efekt ten nazywamy aliasingiem nieodtwarzalnym. Pojęcie „aliasing” wywodzi się bowiem stąd, że — zgodnie ze wzorem (3.8) — widmo sygnału spróbkowanego składa się z właściwego widma sygnału ciągłego oraz z jego poprzesuwanych „aliasów” (obrazów).