62106 P1111266

38 VIII. Funkcja pierwotna (całka nieoznaczona)

Odpowiedź:

2x¹—6x¹+Sx— 9 (x¹-2x+2)^a

^+l0'^l₂}+2' ⁺2 aK tg (x~^1)+C■

*>/

(at+U^at³+¹+!)¹

Wydzielając część wymierną całki otrzymujemy

Ql - (*+D (*»+*+l)^a, Q₂ = (*+1) (A:³-ł-A:+l) . Rozkładu szukamy w postaci

C UA^+ÓA^+CAT^3+</^1+^1 V /jc^3+<7AT+A
L (Ar+I)(AT^3+A:f l)^3 J (a;+1)(x^3+x+1)
Z układu równań
*^ł	/=o,
	-o+p = i,
*^s	o—2ó+3p+A = —1 ,
X^4	5a-ó-3c+5p+3A = I,
X^1	4a+3b-3c-4<t+5g+5h - 2,
W	3ó+c-5d~5e-f-3p+5ń = 3,
x^l\	2c—d—7e+g+3h - 3 ,
x°\	d-3e+h = 3
znajdujemy

a - -1, ó = 0, c = —2, <*= 0, e— -1, f — g =h —0. Tak więc całka sprowadza się tu do funkcji wymiernej

SU 2*^a+l _c

(x+l)(x²+x+l)²    *

§ 3. Całkowanie pewnych wyrażeń zawierających pierwiastki

278. Całkowanie wyrażeń postaci (x, |/(a¹+/?)/(a¹-f<5)) (¹)• Nauczyliśmy się już całkować w postaci skończonej różniczki wymierne. W dalszym ciągu zasadniczym sposobem całkowania różnych klas wyrażeń różniczkowych będzie znalezienie takich podstawień / — co (x), które sprowadzają wyrażenie podcałkowe do postaci wymiernej i umożliwiają przedstawienie całki jako funkcji / w postaci skończonej. Jeśli przy tym sama funkcja co (¹), którą należy podstawić za /, wyraża się przez funkcje elementarne, to całka wyrazi się również jako funkcja x w postaci skończonej.

Sposób ten nazwiemy metodą sprowadzenia wyrażenia podcałkowego do postaci wymiernej.

Jako pierwszy przykład jej zastosowania rozpatrzymy całkę postaci

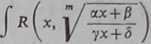
dx ,

gdzie R oznacza funkcję wymierną dwóch argumentów, m — liczbę naturalną, a a, 0, y, 5 są stałymi. Podstawmy

_tm - **+/?

yx+b ’

x

= <p (0 =

5t^M-p ct—y t^M

Całka (1) przejdzie w całkę

fR(v(0.0r'C0dt;

tu różniczka ma już postać wymierną, gdyż R, <p, <p' są funkcjami wymiernymi. Obliczywszy tę całkę według reguły poprzedniego paragrafu, powrócimy do starej zmiennej podstawiając z powrotem t = co (pc).

Do całki (1) sprowadzają się także ogólniejsze całki

/■H3)'    ^:■■

gdzie wszystkie wykładniki r, s,... są wymierne. Wystarczy tylko wszystkie te wykładniki sprowadzić do wspólnego mianownika m, by otrzymać pod znakiem całki funkcję wymierną zmiennej x i pierwiastka \/(cix+P)l(yx+5).

Przykłady.

i) f —Y*±l±ł—dx

Tutaj funkcja wymierna ■    sprowadziła się po prostu do funkcji liniowej. Przyjmijmy

/ = y x-1-1, dx~* 2tdt, wówczas

J    ^J f³-¹    j\'-l

arctg + C,

r+r+1    y 3

pozostaje tylko podstawić jeszcze / — y/jr+l7

i    /• »r

i

r dx    f J/ x+l .

yu-i)(x+i)

Przyjmujemy

i.,V£±L.    *

l* + l .

#*—* I '    (**-!)*

1

Umawiamy się raz na zawsze oznaczać literą /? funkcję wymierną swoich argumentów.