Image12 (39)

113

P₂

Rozwiązania zadań ze zbioru "MENDLA

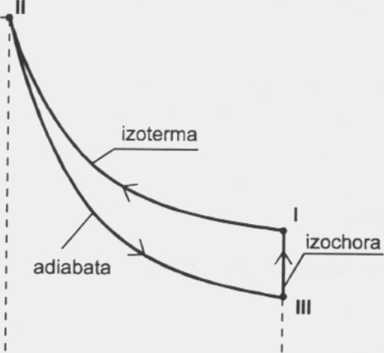
^vi=V₃ V

Rozwiązania zadań ze zbioru "MENDLA

114

T₂= 500K

Ze stanu I do stanu II gaz jest przeprowadzony izotermicznie, więc:

T₁ = T₂ = 500K

Z równania Clapeyrona dla stanu trzeciego otrzymamy temperaturę T3.

^^V- = n • R / • T₃ 13

p₃ . V₃ = n • R • T₃ /: n ■ R

T₃ =

P3 • V3 n- R

lecz

m

n = — P

_a z wykresu mamy V₃ = Vi = 0,01/rr³ po podstawieniu do T3 będzie:

P3 • Vi

T3 =

t₃ =

Z równania Clapeyrona dla stanu drugiego otrzymamy:

^V? = _n • R /-T₂ I 2

p2 • V₂ = n • R • T₂ /: (n • R)

P2 • V2

stąd T₂ =

n ■ R

Ilość moli gazu n możemy obliczyć dzieląc masę gazu m przez masę jednego mola n tego gazu.

m

n =

Po podstawieniu do temperatury T₂ mamy: P2 • V₂

t₂ =

T2 =

T2 =

— • R P

P2 • V2•P m • R

2,6 • 10⁷ Pa ■ 0,005 m³ ■ 0,032-^-,

mol

1 kg 8,31

J

Pa- —

rrł

J= N-m

T3 =

T3 =

— • R P

P3 • Vi•P m • R

10⁷ Pa-0,01 nr? - 0,032 ^ mol

^■⁸'³¹żrb

3200-^3 -rr?-^³-

8,31^^

K • mol

T₃ = 385

N ■ m • kg K • mol

_Pa-_Ł

³ nf

J= N ■ m

mol kg ■ N ■ m

T₃ = 385AC

Ze stanu I do II gaz jest przeprowadzony izotermicznie, więc: Ti = T₂ = 300K. Dla tej przemiany mamy:

pi • Vi = p₂ • V₂ /: Vi

Pi =

Pi =

P2 • V2 Vl

2,6 - 10⁷ 0,005 m³

K ■ mol

T2 =

0,000416-10⁷Az-n?.^³-_l rr? ™>l

8,31

kg • N ■ m K ■ mol

T2 = 500^^m/(g. ^K'^mo1 mol kg ■ N ■ m

0,01 m³ pi = 1,3 • 10⁷Pa pi = 13-10 ⁶Pa pi = 13 MPa

Odp.: Temperatura tlenu w kolejnych stanach wynosiła: 500K, 500K, 385/C. Ciśnienia dla stanu pierwszego: 13MPa, a objętość w stanie trzecim 0,01 m³.