Image70 (6)

138

\

znajdujemy, że maksymalna wartość o odpowiada kątowi

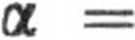
arc cos

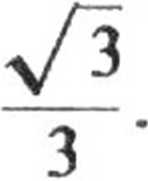
2.98. Siła tarcia T_t pojawiająca się w momencie zetknięcia obręczy z podłożem, wywołuje zmiany jej prędkości liniowej i kątowej. Zgodnie z II zasadą dynamiki zmiany te opisane są równaniami:

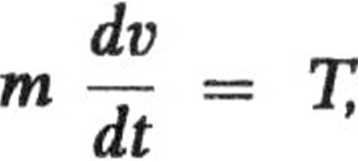
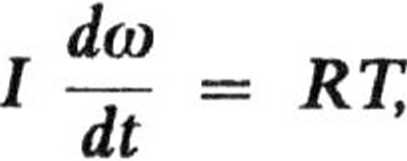
gdzie: I = mR² jest mo równań czas dostajemy

II

entem bezwładności pierścienia. Eli

II

inując z tych

dv

Rdco.

Całkując to równanie w granicach od prędkości początkowej v_Q do końcowej — v_k i od prędkości kątowej w_Q do końcowej co_k = odpowiadającej toczeniu

R

bez poślizgu, otrzymujemy

v.

~ ».)

Aby obręcz toczyła się do tyłu, musi być spełniony warunek

0)_o R > v„.

II. MECHANIKA RELATYWISTYCZNA

3. EFEKTY KINEMATYCZNE TRANSFORMACJI LORENTZA

3.1. Korzystając z transformacji Lorentza mamy

2 _

c²t² - v" — (    ct — ) + x)

1 + P

I - R

(ct' + x')

+ p

p

(ct' — x') =

c²t!² — x'².

Podobnie

c²At²

Ax

(cAt

Ax) (cAt -f Ax) =

1

1 + P

P

(cAf + Ax')

i - p

i + p

(icAt' — Ax') = c^zAt

rl

Ax

12

3.2. Po zróżniczkowaniu równań transformacji Lorentza otrzymujemy

dx

y (dx' + Vdt'),

dy

dy\

dz = dz',

dt =

y \dt^r + ~ dx'

Wobec tego

ds² = y² [ 1

V

dx^,2+ dy'² + dz

>2.

12

c²y² ( 1

V

dt'² =

= dx'² -f dy'² -f dz'² — c² dt'² = ds 12