Przetwarzanie Sygnałów 2 Laboratorium	Ćwiczenie nr. 8 „Zera i bieguny filtru a jego OI i transmitancja”
Damian Sosnowski 129003 Wydział Elektroniki Mikrosystemów i Fotoniki Środa 7:30	Data Ćwiczenia: 1.XII. 2004	Ocena:

1. Wyznaczanie pierwiastków wielomianów z wykorzystaniem funkcji roots(argument)

1. 
   

zdefiniowałem z = [1 -1 0,5] roots(z) otrzymałem 2 pierwiastki:

2. 
   

zdefiniowałem z = [1 -2 2] roots(z) otrzymałem 2 pierwiastki:

3. 
   

zdefiniowałem z = [1 1 0,5] roots(z) otrzymałem 2 pierwiastki:

4. 
   

zdefiniowałem z = [1 2 2] roots(z) otrzymałem 2 pierwiastki:

e)

zdefiniowałem z = [1 -i 0,5] roots(z) otrzymałem 2 pierwiastki:

f)

zdefiniowałem z = [1 -1,5-1,5i i] roots(z) otrzymałem 2 pierwiastki:

Zauważyłem, że pierwiastkami równań
,
,
i
są liczby sprzężone, natomiast pierwiastkami wielomianu
były tylko liczby urojone, a pierwiastki wielomianu
mają tą właściwość, że cześć rzeczywista pierwiastka jest równa co do wartości ujemnej części urojonej, czyli zachodzi równość:

2. Wyznaczanie współczynników wielomianów przy pomocy funkcji poly(argument)

W tym zadaniu chodzi o podanie 2 liczb które są pierwiastkami określonego wielomianu w postaci macierzy jednostkowej, a funkcja poly(arg) zwróci nam 3 liczby a b c, które są współczynnikami wielomianu

1. 
   

zdefiniowałem z = [0.5+0.5i 0,5-0,5i] poly(z) i otrzymałem wielomian:

2. 
   

zdefiniowałem z = [1+i 1-i] poly(z) i otrzymałem wielomian:

3. 
   

zdefiniowałem z = [-0.5+0.5i -0,5-0,5i] poly(z) i otrzymałem wielomian:

4. 
   

zdefiniowałem z = [-1+i -1-i] poly(z) i otrzymałem wielomian:

5. 
   

zdefiniowałem z = [0.5+0.5i -0,5+0,5i] poly(z) i otrzymałem wielomian:

6. 
   

zdefiniowałem z = [0.5+0.5i 1+i] poly(z) i otrzymałem wielomian:

Zauważyłem, że wielomian
,
,
i
miały współczynniki rzeczywiste, natomiast dwa pozostałe wielomiany
i
miały współczynniki zespolone. Niektóre z podanych pierwiastków były pierwiastkami wielomianów z zadania 1, więc teraz wyznaczając za pomocą ich współczynników wielomianów dokonałem sprawdzenia poprzednich obliczeń i otrzymałem te same wielomiany co w zadaniu 1

3. Badanie wpływu położenia pary sprzężonych biegunów na przebieg sygnału:

Wybrałem 3 sprzężone względem siebie bieguny lezące po stronie osi dodatniej:

Zdefiniowałem sygnał x będący pobudzeniem filtru, który początkowo ma wartość 1, a potem tylko 0 zrealizowałem go za pomocą macierzy:

x1 = zeros(1,100);

x =[1 x1];

Badałem wpływ położenia biegunów sprzężonych względem koła jednostkowego z = 1 na stabilność tego filtru:

wewnątrz okręgu jednostkowego:

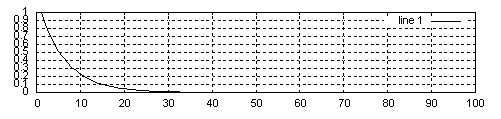
Gdy bieguny sprzężone znajdują się wewnątrz okręgu jednostkowego to układ jest stabilny.

na okręgu jednostkowym:

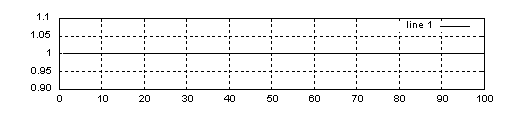
Jeśli bieguny sprzężone położone są bezpośrednio na kole jednostkowym to układ pracuje jak generator.

poza okręgiem jednostkowym:

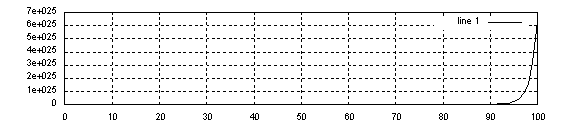
Jeśli bieguny sprzężone znajdują się poza okręgiem jednostkowym to układ jest niestabilny.

4. Wyznaczenie charakterystyki częstotliwościowej układu:

Transmitancja układu była zadana wzorem:

• Zdefiniowałem współczynniki wielomianów:

A=[1 -1 0.5] B=[1 1 0.5]

Obliczam zera i bieguny układy korzystając z funkcji roots:

a = roots(A)

b = roots(B)

Definiuje pobudzenie filtru x, które w początkowo ma wartość 1, a potem tylko 0 zrealizowałem to za pomocą macierzy:

x1 = zeros(1,100);

x =[1 x1];

Obliczam odpowiedź filtru w dziedzinie częstotliwości, korzystając z funkcji freqz i przyrównuje ją do wektora C

C= freqz(filter(a,b,x))

Otrzymaną odpowiedź filtru w dziedzinie częstotliwości wykreślam na wykresie:

Rysunek przedstawia charakterystykę częstotliwościową układu, maksimum znajduje się wokół wartości 140 Hz.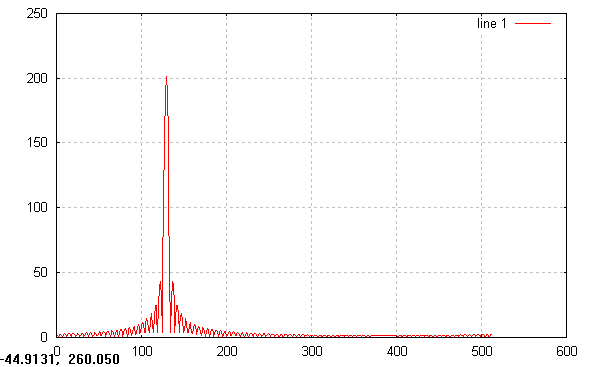

2

---