Przetwarzanie Sygnałów 2 Laboratorium	Ćwiczenie nr. 1 „Funkcja autokorelacji i korelacji wzajemnej”
Damian Sosnowski 129003 Wydział Elektroniki Mikrosystemów i Fotoniki Środa 7:30	Data Ćwiczenia: 17. XI. 2004	Ocena:

1. Wyznaczenie estymat funkcji autokorelacji sinusoidy z losową fazą początkową:

Zbadany sygnał to : Sinusoida z losową fazą początkową i składową stałą

y =2 + sin (2πft + φ) gdzie φ to zmienna losowa o rozkładzie jednostajnym na przedziale [-π,π]

Ustawiona długość autokorelacji N = 100

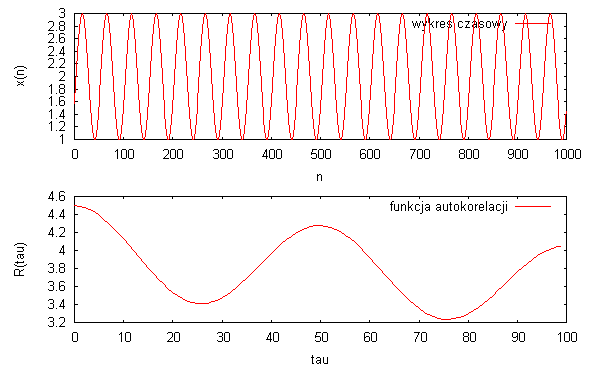
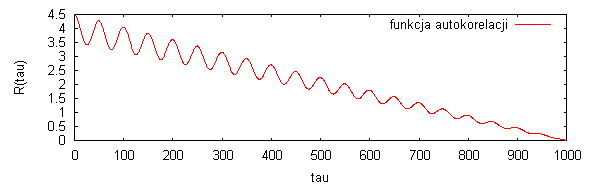
Ustawiona długość autokorelacji N = 1000

2. Wyznaczenie funkcji autokorelacji dla szumu białego oraz korelacji wzajemnej pomiędzy szumem białym a szumem białym z echem:

Skrypt zastosowany w ćwiczeniu generował szum biały, następnie przepuszczał przez układ liniowy o zadanej odpowiedzi impulsowej, który do wyjściowego sygnału dodawał echo, charakteryzujące się tym, że sygnał był przesunięty o 4 próbki i stłumiony 2 razy oraz przesunięty o 8 próbek i stłumiony 4 razy.

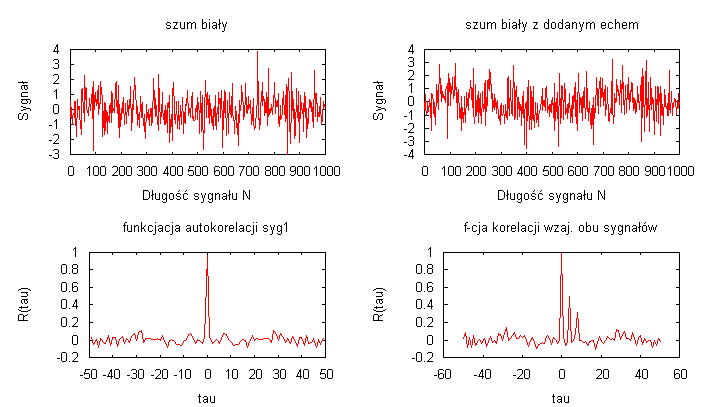
Liczba próbek sygnału szumu N=200, długość korelacji wzajemnej Ncor = 50

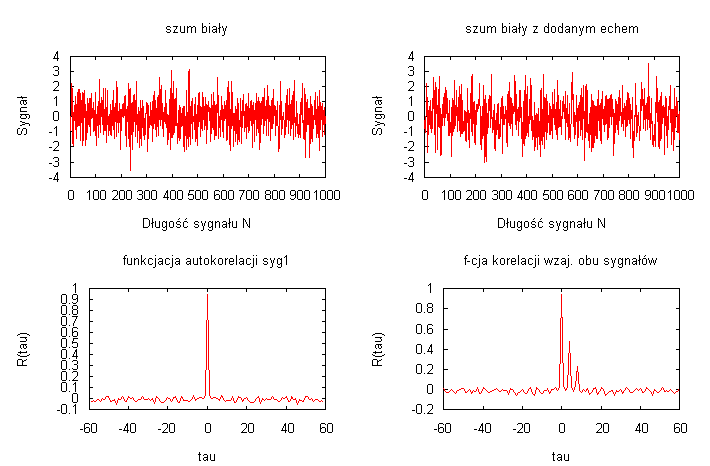
Liczba próbek sygnału szumu N=2000, długość korelacji wzajemnej Ncor = 50

3. Zbadanie estymat funkcji autokorelacji dla sygnału mowy:

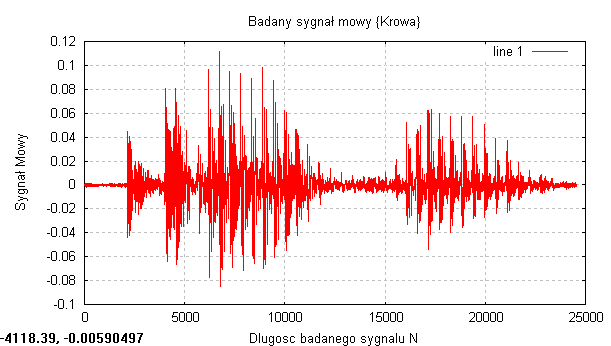
Analizowanym przeze mnie sygnałem był sygnał mowy „Krowa”

Zbadałem funkcje autokorelacji dla pierwszej połowy sygnału mowy, jej przebieg obrazuje poniższy wykres:

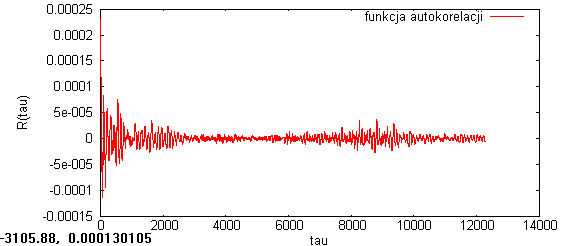
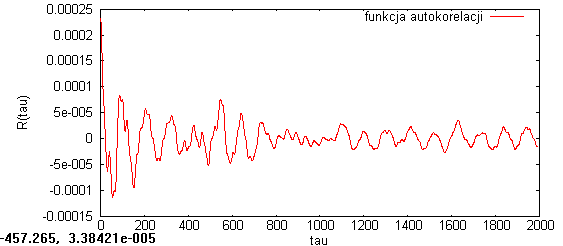
Dokonałem analizy dla fragmentu sygnału mowy w przybliżeniu stacjonarnego

4. Wnioski:

Pierwszym badanym sygnałem była sinusoida z losową fazą początkowo. Do tego sygnału dodałem składową stałą. Na podstawie skończonego zbioru obserwacji (próbek sygnału) możliwe jest oszacowanie (estymacja) funkcji autokorelacji. Funkcja Autokorelacji R(τ) określona jest jako wartość oczekiwana iloczynu zmiennej losowej x(n) w chwili n i tej samej zmiennej losowej przesuniętej w dziedzinie czasu x(n+τ). Za pomocą programu GNU Octave wykreślałem zależność autokorelacji dla sygnałów o różnej liczbie próbek. Analizę przeprowadziłem dla sygnałów sinusoidalnych o liczbie próbek 10,100,1000 i analizowałem jak zmieni się kształt funkcji autokorelacji przy zwiększaniu liczby próbek Ze względu na dużą wielkość wykresów w sprawozdaniu zamieściłem tylko jeden dla sygnału o N=1000 próbek. Zauważyłem, że zwiększanie liczby próbek powoduje wzrost globalnego maksimum funkcji autokorelacji w punkcie τ , wartość w tym punkcie tym rośnie bo jest wartością średniokwadratową wartości oczekiwanej. Największe zmiany funkcja autokorelacji ma w okolicy maksimum τ = 0 dlatego, że średniokwadratowe wartości oczekiwane są w okolicy maksimum największe, przedstawiłem to na wykresie (długość autokorelacji 100). Na wykresie gdzie długość autokorelacji wyniosła 1000 widać swobodny spadek średniokwadratową wartości oczekiwanej do 0 (dla punktu τ = 1000).

Wyznaczona funkcja autokorelacji dla szumu białego oraz funkcja korelacji wzajemnej pomiędzy szumem białym a szumem białym z echem doskonale obrazuje na wykresach własności funkcji autokorelacji i funkcji korelacji wzajemnej dla tych sygnałów. Na wykresach widać parzystość funkcji autokorelacji, globalne maksimum występuje w zerze, które rośnie jeśli zwiększana jest liczba próbek sygnału szumu. Długość autokorelacji przyjąłem jako 50, bo wartości funkcji autokorelacji mają najbardziej istotne zmiany pomiędzy wartościami 0 i 50. Wyznaczyłem obydwie funkcja korelacji wzajemnej R_XY i R_YX

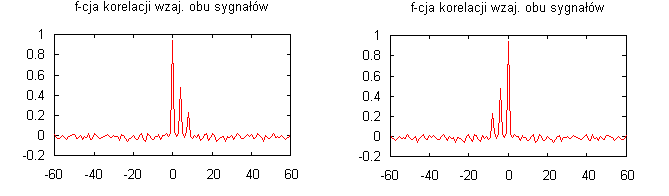
Spełniają one własności R_XY(τ) = R_YX(-τ) oraz posiadają globalne maksimum w zerze.

Następnym badanym sygnałem był sygnał mowy. Wykreśliłem funkcje autokorelacji dla połowy sygnału oraz dla obszaru początkowego sygnału (od 0 do 2000 próbek) ten fragment w przybliżeniu można było uznać za stacjonarny. Ponownie zauważamy globalne maksimum w zerze a dla dalszych punktów nie ma znaczących zmian. Przy funkcji autokorelacji w zakresie od 0 do 12500 próbek widać, że estymacja autokorelacji, ze względu na losowe zmiany wartości w całym sygnale nie może być wyznaczana na dowolnym przedziale próbek.

4

---