ANALIZA STATYSTYCZNA
z wykorzystaniem techniki komputerowej
Analiza statystyczna z wykorzystaniem pakietu
Microsoft Excel
Graficzna prezentacja danych statystycznych nie wymagających specjalnej obróbki statystycznej
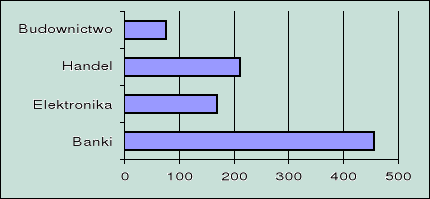
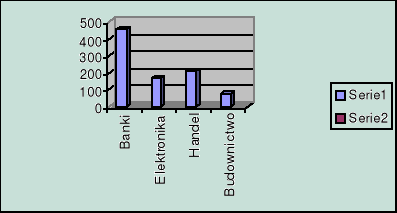
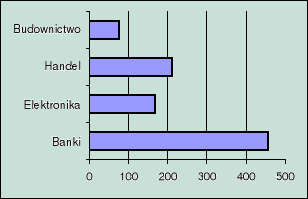
Dane o portfelu akcji
Banki |
Elektronika |
Handel |
Budownictwo |
456,2 |
168,3 |
211,1 |
76,9 |
Wykres kołowy
(wykonany przy pomocy Kreatora wykresów)
Inne formy prezentacji
Wykres kolumnowy
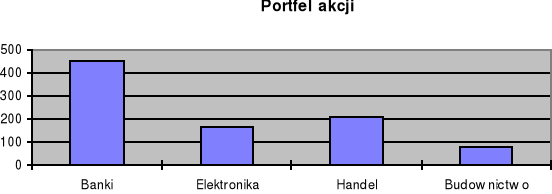
Wykres słupkowy
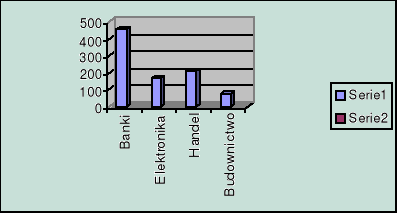
Wykres trójwymiarowy
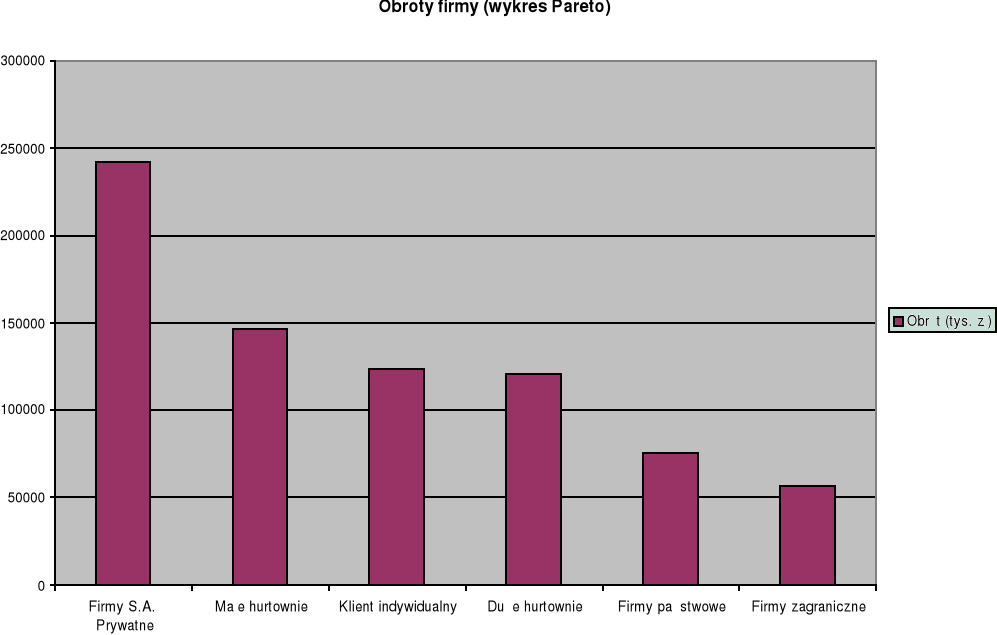
2. Graficzna prezentacja danych statystycznych ze wstępną obróbką statystyczną (wykres Pareto)
Rodzaj |
Liczba |
Obrót (tys. zł) |
Klient indywidualny |
2200 |
123400 |
Małe hurtownie |
183 |
146578 |
Duże hurtownie |
16 |
120600 |
Firmy państwowe |
28 |
76000 |
Firmy S.A. Prywatne |
34 |
242000 |
Firmy zagraniczne |
4 |
56300 |
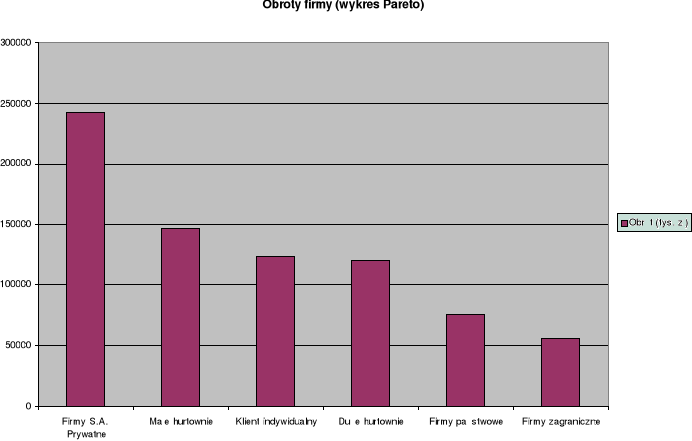
Prezentacja szeregów rozdzielczych
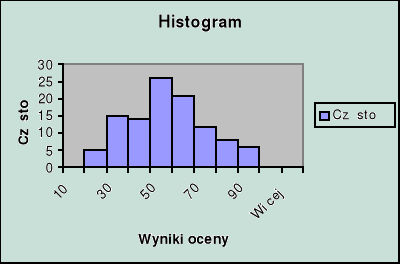
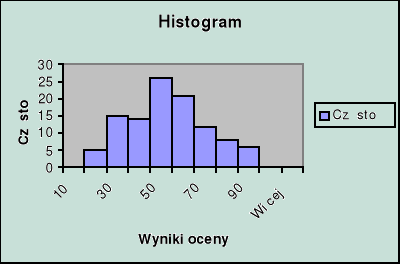
Histogramy
populacja: 40 - 60 jednostek - liczba klas (grup): 6 - 8
populacja: 60 - 100 jednostek - liczba klas (grup): 7 - 10
populacja: 100 - 200 jednostek - liczba klas (grup): 9 - 12
populacja: 200 - 500 jednostek - liczba klas (grup): 12 - 17
Wzór Sturgesa na liczbę klas (grup, przedziałów)
Histogram: zbiór przylegających prostokątów, których podstawy - równe rozpiętości przedziałów klasowych - spoczywają na osi odciętych, a wysokości odpowiadają liczebnościom (częstościom) danych przedziałów.
Tworzenie histogramu przy pomocy Excela
Tablica danych (np. kolumna arkusza o adresach $B$2:$B$102)
Tablica wartości granic poszczególnych klas (np. kolumna arkusza o adresach $D$2:$D$10)
Użyć opcji Narzędzia|Analiza danych..|Histogram
W oknie dialogowym określić
Zakres komórek (danych) - np. $B$2:$B$102
Zakres zbioru (granic klas) - np. $D$2:$D$10
Miejsce histogramu (komórka w arkuszu | nowy arkusz | nowy skoroszyt)
Wykres wyjściowy (zaznaczyć)
Utworzyć histogram
Dokonać edycji histogramu (np. przylegające do siebie słupki uzyskujemy w następujący sposób:
„klikamy” prawym przyciskiem myszy na rysunku dowolnego słupka
wybieramy Formatuj serię danych|Opcje
ustaw szerokość przerwy na 0.)
Dokonaj dalszej edycji histogramu (rozmiar, tytuły, legenda, itp.)
Na arkuszu, na którym narysowany jest histogram utworzona zostaje tabela o postaci, np.
Granice klas |
Częstość |
10 |
0 |
20 |
5 |
30 |
15 |
40 |
14 |
50 |
26 |
60 |
21 |
70 |
12 |
80 |
8 |
90 |
6 |
100 |
0 |
Więcej |
0 |
Prosta analiza danych statystycznych
Miary położenia (wartości przeciętne)
Wartość średnia (populacji, próby)
Mediana (Me): dzieli zbiór danych (populację, próbę) na dwie połowy;
C) Kwartyle (Q1, Q2 (Me), Q3): oddzielają ćwiartki.
Wartość modalna (moda, dominanta): wartość w zbiorze danych, która w danym rozkładzie empirycznym występuje najczęściej.
Miary zmienności (rozrzutu)
Wariancja
Wariancja w zbiorze danych (populacji)
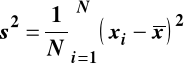
Wariancja w próbie losowej
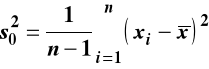
Odchylenie standardowe
Odchylenie standardowe w zbiorze danych (populacji)
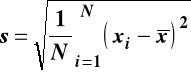
Odchylenie standardowe w próbie losowej
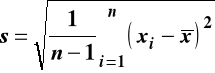
Rozstęp (w populacji, w próbie)
![]()
Miary asymetrii i spłaszczenia
Współczynnik asymetrii (skośności)
Dla zbioru danych (populacji)
gdzie
Dla próby losowej
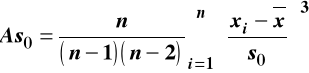
Współczynnik koncentracji (kurtoza)
Dla zbioru danych (populacji)
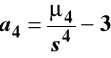
gdzie
Dla próby losowej
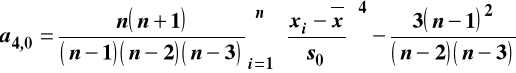
Statystyczny opis danych przy pomocy Excela
Wykorzystanie opcji:
Narzędzia | Analiza danych | Statystyka opisowa
Wybrać zakres danych (zakres wejściowy)
Wybrać opcję Statystyki podsumowujące
Wykonać obliczenia
Charakterystyka |
Nazwa w Excelu |
Wzór dla populacji |
Wzór dla próby |
Wartość średnia |
Średnia |
X |
X |
Błąd oceny wartości średniej |
Błąd standardowy (średniej) |
|
X |
Mediana |
Mediana |
X |
X |
Wartość modalna |
Tryb (!!!???) |
X |
X |
Odchylenie standardowe |
Odchylenie standardowe |
|
X |
Wariancja |
Wariancja próbki |
|
X |
Współczynnik koncentracji |
Kurtoza |
|
X |
Współczynnik asymetrii |
Skośność |
|
X |
Rozstęp |
Zakres (!!??) |
X |
X |
Wartość minimalna |
Minimum |
X |
X |
Wartość maksymalna |
Maksimum |
X |
X |
Suma wartości |
Suma |
X |
X |
Liczność (zbioru, próby) |
Licznik (!!??) |
X |
X |
Wykorzystanie funkcji statystycznych Excela
Charakterystyka |
Funkcja statystyczna |
Wartość średnia |
ŚREDNIA (zakres danych) |
Wariancja (w populacji) |
WARIANCJA.POPUL(zakres danych) |
Wariancja (w próbie) |
WARIANCJA(zakres danych) |
Odch. Standardowe (w populacji) |
ODCH.STANDARD.POPUL(zakres danych) |
Odch. Standardowe (w próbie) |
ODCH.STANDARD(zakres danych) |
Mediana |
MEDIANA(zakres danych) |
Wartość modalna |
WYST.NAJCZĘŚCIEJ(zakres danych) |
Kwartyl |
KWARTYL(zakres danych, nr kwartyla) |
Współczynnik asymetrii w próbie |
SKOŚNOŚĆ(zakres danych) |
Współczynnik koncentracji (kurtoza) w próbie |
KURTOZA(zakres danych) |
Wartość minimalna |
MIN(zakres danych) |
Wartość maksymalna |
MAX(zakres danych) |
W powyższej tabeli przez „zakres danych” rozumie się zbiór (do 30 elementów) zakresów danych w arkuszu (adresów), pojedynczych liczb, nazw tablic.
Inne charakterystyki opisujące dane statystyczne
Średnia geometryczna
Średnia harmoniczna
Odchylenie przeciętne
Percentyle
Wartości statystyk pozycyjnych
Średnia obustronnie ucięta
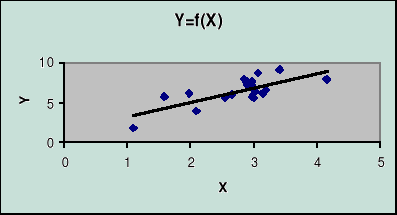
Badanie prostych zależności stochastycznych
Symbolem Y oznaczamy zmienną zależną (objaśnianą), zaś symbolem X zmienną niezależną (objaśniającą). Zależność stochastyczna występuje wtedy gdy wraz ze zmianą wartości jednej zmiennej zmienia się rozkład prawdopodobieństwa drugiej zmiennej.
Dane:
Zmienna X: x1,x2, .... ,xn
Zmienna Y: y1,y2, .... ,yn
Pole rozrzutu (wykonane kreatorem wykresu)
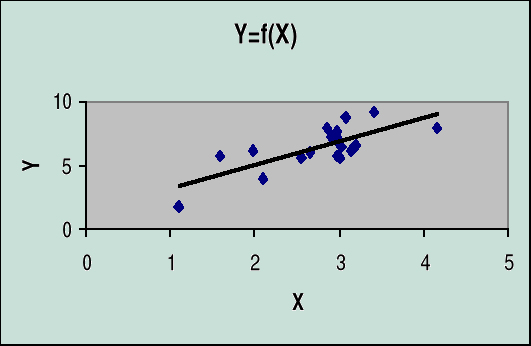
Liczbowe miary zależności stochastycznej
Kowariancja
Wyznaczamy oszacowanie kowariancji zmiennych losowych X i Y:
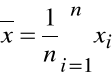
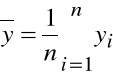
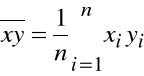
Kowariancje obliczamy wykorzystując opcję:
Narzędzia | Analiza danych | Kowariancja
|
Kolumna 1 |
Kolumna 2 |
Kolumna 1 |
0,443634 |
|
Kolumna 2 |
0,826663 |
2,66128 |
Współczynnik korelacji liniowej Pearsona
gdzie s(x) oraz s(y) są odchyleniami standardowymi zmiennej X oraz Y
Interpretacja: r=0 - brak zależności liniowej; - dodatnia zależność liniowa; - ujemna zależność liniowa.
Współczynnik korelacji obliczamy wykorzystując opcję:
Narzędzia | Analiza danych | Korelacja
|
Kolumna 1 |
Kolumna 2 |
Kolumna 1 |
1 |
|
Kolumna 2 |
0,760801 |
1 |
Wykorzystanie funkcji statystycznych Excela do wyznaczania miar zależności
Charakterystyka |
Funkcja statystyczna |
Kowariancja |
KOWARIANCJA (tabela1;tabela2) |
Współczynnik korelacji |
WSP.KORELACJI(tabela1;tabela2) |
Analiza regresji
W wielu przypadkach spotykanych w praktyce interesuje nas zależność obserwowanej zmiennej losowej (zmiennej zależnej) Y od wartości jakie przyjmuje inna zmienna (nie koniecznie losowa), zwana zmienną niezależną X. Zmienną zależną Y nazywamy czasami zmienną objaśnianą, a zmienną niezależną X nazywamy wówczas zmienną objaśniającą. Interesują nas zazwyczaj przypadki gdy zależność ta ma postać liniową
gdzie jest zmienną losową (zakłóceniem) o zerowej wartości oczekiwanej i stałej wariancji.
Linię regresji uzyskujemy na wykresie pola rozrzutu przez uaktywnienie opcji „Linia trendu”
Zastosowanie opcji
Narzędzia | Analiza danych | Regresja
powoduje wyświetlenie nieczytelnych informacji, które nie nadają się do praktycznego wykorzystania.
Parametry funkcji regresji przedstawionej w postaci
Y=m*x+b
można obliczyć wykorzystując funkcję
REGLINP(tablica_Y;tablica_X;const;stats)
const : (=PRAWDA, dowolne b; =FAŁSZ, b=0)
stats : (=PRAWDA, to obliczane są dodatkowe charakterystyki; =FAŁSZ lub pominięte, to obliczane są tylko parametry funkcji regresji)
Parametry funkcji regresji uzyskujemy wywołując funkcje:
Parametr m:
INDEKS(REGLINP(tablica_Y;tablica_X;const;stats);1;1)
NACHYLENIE(tablica_Y;tablica_X)
Parametr B:
INDEKS(REGLINP(tablica_Y;tablica_X;const;stats);1;2)
ODCIĘTA(tablica_Y;tablica_X)
5. Wnioskowanie statystyczne
z wykorzystaniem pakietu
Microsoft Excel
5.1 Estymacja punktowa parametrów rozkładów prawdopodobieństwa
Można wykorzystać funkcje Excela tylko w najprostszych przypadkach, na przykład
wartość oczekiwana w rozkładzie normalnym
funkcja ŚREDNIA(tablica_danych)
odchylenie standardowe w rozkładzie normalnym
funkcja ODCH.STANDARDOWE(tablica_danych)
5.2 Estymacja przedziałowa parametrów rozkładów prawdopodobieństwa
Przypadek wartości oczekiwanej rozkładu normalnego o znanej wartości odchylenia standardowego; dwustronny przedział na poziomie ufności
Korzystamy z funkcji
ŚREDNIA(tablica_danych)
UFNOŚĆ(poziom_istotności;odchyl_stand;liczn_próbki)
gdzie
poziom_istotności =
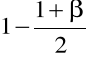
odchyl_stand = σ
liczn_próbki = n
Granice przedziału ufności :
dolna: ŚREDNIA(tablica_danych) - UFNOŚĆ(poziom_istotności;odchyl_stand;liczn_próbki)
górna: ŚREDNIA(tablica_danych) + UFNOŚĆ(poziom_istotności;odchyl_stand;liczn_próbki)
W przypadkach innych przedziałów ufności dla parametrów rozkładu normalnego lub w przypadku innych rozkładów prawdopodobieństwa należy korzystać z odpowiednich formuł matematycznych pakietu Excel oraz funkcji do obliczania kwantyli rozkładów.
Przykład: Przedział ufności dla wartości oczekiwanej rozkładu normalnego o nieznanej wartości odchylenia standardowego; dwustronny przedział na poziomie ufności
gdzie tn-1,(1+)/2 jest kwantylem rzędu (1+ w rozkładzie t-Studenta o n-1 stopniach swobody (stabelaryzowany)
Korzystamy z funkcji:
ŚREDNIA(tablica_danych)
ODCH.STANDARDOWE(tablica_danych)
ROZKŁAD.T.ODW(poziom_ufności; stopnie_swobody)
O.Hryniewicz: Analiza statystyczna - komputery (8 godz.) 17
Wyszukiwarka
Podobne podstrony:
AnaLIZA STATYSTYCZNA 8 wykład6, 1
AnaLIZA STATYSTYCZNA 8 wykład2, ANALIZA STATYSTYCZNA
AnaLIZA STATYSTYCZNA 8 wykład3, ANALIZA STATYSTYCZNA
AnaLIZA STATYSTYCZNA 8 wykład7, 1
AnaLIZA STATYSTYCZNA 8 wykład4, Analiza statystyczna z wykorzystaniem pakietu
Wykład 4 analiza struktury, Statystyka opisowa
AnaLIZA STATYSTYCZNA 8 wykład4 rysunki
AnaLIZA STATYSTYCZNA 8 wykład5, Analiza statystyczna z wykorzystaniem pakietu
Wykład 2-Opisowa analiza zjawisk masowych, socjologia, statystyka
Metodologia z elelmentami statystyki dr Izabela Krejtz wyklad 7 Wprowadzenie do analizy war
więcej podobnych podstron