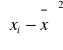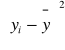Klasyfikacji i uporządkowaniu wartości badanej cechy np. miejsce zamieszkania, porządek alfabetyczny, odległość od danego miejsca.
PRZEDZIAŁOWA (interwałowa) Dotyczy cech ilościowych. Przedziały mają ustaloną długość. Brak stałego zera, np. skale temperaturowe
STOSUNKOWA (proporcjonalna) lub ILORAZOWA Dotyczy cech ilościowych i przedziały mają ustaloną długość, zero jest absolutne i ma takie znaczenie jak w zbiorze liczb.
ad. III. Rodzaje ankiety
W ankiecie musi być wyróżniona część pytań dotyczących cech stałych i zmiennych
Rodzaje pytań:
- zamknięte (a, b, c)
- otwarte (wpisz odpowiedź)
ad. IV. Rodzaje kontroli:
Formalna - dotyczy odpowiedzi na pytania o cechy stałe
Merytoryczna - dotyczy odpowiedzi na pytania o cechy zmienne
ad. V. Opracowanie i prezentacja
Trzy formy prezentacji:
szeregi statystyczne
tabele
wykresy
Podział szeregów statystycznych:
szczegółowe - wyliczające
rozdzielcze - strukturalne
dla cechy mierzalnej ilościowej:
- punktowe
- przedziałowe
dla cechy niemierzalnej jakościowej
przestrzenne
czasowe:
szeregi momentów
szeregi okresów
Ilustracje
szereg szczegółowy wyliczający : 25, 34, 45, 24, 34, 25, 45 (czas dojazdu w min.)
symbol: liczba elementów w grupie n, N
n = 7 (siedem obserwacji)
Jeśli próby są duże, obserwacje się powtarzają budujemy szeregi rozdzielcze.
Rozdzielamy informacje o wartościach w próbie z informacją o tym ile razy ta wartość się powtarza.
Szereg rozdzielczy punktowy
x i |
n i |
5 |
3 |
34 |
2 |
45 |
2 |
x i - ciąg wartości (wartości obserwowanej cechy)
n i - liczebności z jaką występują badane wartości
n 1 + n 2 + n 3 = 7
Szereg rozdzielczy przedziałowy
< x i x i+1 > |
n i |
4-6 6-8 8-10 10-12 |
12 10 8 6 |
|
36 |
![]()
Podział na przedziały nazywamy AGREGACJĄ INFORMACJI
Szereg czasowy okresów
t i |
y i |
1998 1990 2000 2001 2002 |
24 25 23 22 23 |
|
|
szereg rozdzielczy szereg czasowy
n i y i
x i t i
Tabele
Tabela statystyczne to więcej niż 1 szereg statystyczny
Wykresy
Poza układem współrzędnych:
- diagram, - wykres słupkowy
w układzie współrzędnych:
- histogram,
- wielobok liczebności
- krzywa liczebności.
Opis i wnioskowanie statystyczne
Opis statystyczny to wykonanie analiz wartości badanych cech obserwowanych w próbie.
analiza struktury zbiorowości
analiza współzależności badanych cech
analiza zmian badanych zjawisk w czasie rzeczywistym
Wnioskowanie statystyczne to metody opisu populacji z wykorzystaniem przeprowadzonych analiz w próbie oraz rachunku prawdopodobieństwa.
Parametry statystyczne są to liczby służące do opisu zbiorowości statystycznej. Stosowane w analizach parametry dzielimy na:
MIARY PRZECIĘTNE
MIARY ZMIENNOŚCI
MIARY ASYMETRII
MIARY KONCENTRACJI
MIARY PRZECIĘTNE
Miary poziomu przeciętnego:
Klasyczne
3 średnie:
Arytmetyczna
Geometryczna
Harmoniczna
Pozycyjne
Dominanta (moda)
Kwantyle
Kwartyl pierwszy
Mediana
Kwartyl trzeci
Jest wypadkową wartości wszystkich obserwacji z próbySuma odchyleń wartości cechy od średniej jest równa zero:
Powiększenie wszystkich wartości w próbie o pewną stałą powiększy średnią arytmetyczną o tę wielkość stałą
Suma wartości zmiennej równa jest iloczynowi średniej arytmetycznej i liczebności próby
Na poziom średniej silny wpływ mają wartości ekstremalne (największa, najmniejsza).
Wskazujemy przedział gdzie jest najwięcej elementów w badanej próbie, gdzie jest dominanta
Wyznaczamy wartość dominanty, wykorzystujemy wzór:
wskazujemy przedział w którym jest dany kwartyl
wyznaczamy przybliżoną wartość posługując się wzorem:
wariancja
odchylenie standardowe
odchylenie przeciętne
współczynnik zmienności
rozstęp
odchylenie ćwiartkowe
współczynnik zmienności
zróżnicowanie
rozproszenie
rodzaj asymetrii
siłę asymetrii
prawostronna (więcej wartości małych)
lewostronna
sym.
prawostronna
lewostronnazależność funkcyjna
-\\- sochastyczna
-\\- korelacyjna
ŚREDNIA ARYTMETYCZNA x
n - wielkość próby
x 1 - wielkość próby
23, 34, 45, 23, 34, 23, 45
ŚREDNIA ARYTMETYCZNA WAŻONA - w szeregu rozdzielczym punktowym
![]()
n - suma liczebności n1
k - liczba wartości cechy w szeregu
![]()
- liczebność i-tej wartości cechy
x i |
n i |
23 34 45 |
3 2 2 |
ŚREDNIA ARYTMETYCZNA WAŻONA - w szeregu rozdzielczym przedziałowym
Przedział (środek przedziału)
n - suma liczebności ![]()
k - liczebność klas (wierszy) w szeregu (przedziale)
![]()
- środek i-tego przedziału
![]()
- liczebność i-tego tego przedziału
<x i x i +1) |
n i |
4-6 6-8 8-10 10-12 |
12 10 18 6 |
Własności średniej arytmetycznej:
Szereg rozdzielczy punktowy
x i |
w 1 |
4 |
0,4
|
5 6 7 |
0,2 0,1 0,3 |
|
1 |
w 1 - częstość względna
Obliczamy następująco: (zawsze licz.większa)
w 1 (zawsze ułamki)
D = 4 (4 różne obserwacje)
n=?
k=
40% obserwacji miało wartość 4
20% -\\- 5
10% -\\- 6
30% -\\- 7
a(b+c) = ab+ac
DOMINANTA (miara pozycyjna) Jest to wartość cechy, która występuje w danej próbie najczęściej
23, 34, 45, 23, 34, 23, 45 D = 23
Dominanta w szeregu rozdzielczym przedziałowym:
Zad. Wyznaczyć dominujący czas eksploatacji maszyn:
Czas [godz] |
Liczba maszyn |
N cum |
wi |
<0,2) <2,4) <4,6) <6,8) <8,10) |
15 40 30 10 5 |
15 55 (15+40) 85 (55+30) 95 (85+10) 100 (95+5) |
0,15 0,4 0,3 0,1 0,05 |
xk - lewy koniec przedziału w którym jest dominanta (2)
x - wartość cechy
n- liczebność (40)
k - przedział dominanty
∆ - długość przedziału, w którym jest dominanta (2)
W badanej próbie czas eksploatacji najczęściej wynosił 3,42 [godz].
Wszystkie miary przeciętne mają jednostkę taką samą jak badana cecha.
Metoda graficzna wyznaczania dominanty - histogram
Mediana - kwantyle
Mediana jest to wartość cechy, która dzieli próbę na dwie części w taki sposób, że połowa wartości jest niewiększa i połowa niemniejsza od mediany (wartość środkowa w próbie)
43, 56, 76, 84, 102
próba ma nieparzystą liczbę elementów wówczas środkowy element istnieje Me = 76
43, 56, 76, 84 parzysta liczba obserwacji
reguła: uśrednij dwa elementy stojące najbliżej środka
Jeżeli próba ma nieparzysta liczbę obserwacji mediana jest równa:
Jeżeli próba ma parzystą liczbę obserwacji:
Porządkujemy rosnąco obserwacje i dopiero wykorzystujemy regułę:
3, 5, 8, 2, 9 2, 3, 5, 8, 9 Me = 5
Szereg rozdzielczy punktowy
x i |
n i |
2 3 4 5 |
1 3 2 1 |
7 obserwacji
x i |
n i |
2 3 4 5 |
1 3 3 1 |
8 obserwacji
Kwartyl pierwszy
Kwartyl pierwszy Q1
Wartość cechy, która dzieli próbę na ... części tak, że 25% 0,25 wartości jest nie większa oraz 75% ¾.
Szereg rozdzielczy przedziałowy Mediana
x - wartość cechy
n - liczebność
k - przedział mediany
xk- lewy koniec przedziału
∆ - długość tego przedziału
Zad. Wyznacz kwartyle czasu eksploatacji maszyn
N cum - ile mamy obserwacji w poprzednim przedziale
Skumulowanie informacji, szukamy liczb 25, 26
Q1 będzie w <2,4)
Q3 będzie w <4,6)
Q2 będzie w <2,4)
¼ badanych maszyn miała czas eksploatacji nie przekraczający 2,5 godz.
½ badanych maszyn miała czas eksploatacji nie przekraczający 3,75 godz.
¼ badanych maszyn miała czas eksploatacji dłuższy niż 5,3 godz.
Graficzna metoda wyznaczenia kwartyli wielobok skumulowanych liczebności
Wykład II
Miary zmienności:
- klasyczne (poziomu przeciętnego, zmienności), wykorzystujemy w rachunkach
- pozycyjne (dominanta)
~ wymiennie do pojęcia zmienności:
dotyczy wartości badanej cechy statystycznej
Porównaj zróżnicowanie wartości w próbach
~ Liczba elementów jest wspólna (dodać element podzielić przez 5)
1, 2, 3, 4, 5
R1=3
Mediana Me = 3
2, 3, 3, 3, 4
R2 = 3
Me = 3
Badając zróżnicowanie wartości cech w próbach statystycznych obserwujemy odległości badanej cechy od średniej arytmetycznej:
- im mniejsze te odległości tym mniejsze zróżnicowanie wartości badanej cechy
W próbie drugiej obserwujemy mniejsze zróżnicowanie wartości badanej cechy
Wariancja to średnia (ważona) kwadratów odchyleń wartości cechy od wartości przeciętnej
Wzory dotyczące wariancji:
Wariancja w szeregu wyliczającym
n - wielkość próby
x1 - wartość badanej cechy w próbie
wariancja dla próby pierwszej
wariancja dla próby drugiej
W próbie drugiej mniejsze zróżnicowanie
Wariancja w szeregu rozdzielczym punktowym
n - suma liczebności
k - liczba wartości cechy w szeregu
ni - liczebność i-tej wartości cechy
Wariancja w szeregu rozdzielczym przedziałowym
n - suma liczebności ni
k - liczba klas (wierszy) w szeregu
![]()
środek i-tego przedziału
ni - liczebność i-tego przedziału
Ze względu na jednostkę miernika jakim jest wariancja wyznaczamy dodatkowo pierwiastek kwadratowy z wariancji, nazywany odchyleniem standardowym
Odchylenie przeciętne jest to średnia (ważona) bezwzględnych odchyleń wartości cechy od wartości przeciętnej
Odchylenie przeciętne w szeregu rozdzielczym przedziałowym
n - suma liczebności n
k - liczba klas (wierszy) w szeregu
![]()
środek i-tego przedziału
ni - liczebność i-tego przedziału
Do wyznaczania zmienności cech statystycznych, których pomiar dokonujemy w różnych jednostkach, wyznaczamy dodatkowo względną miarę względności - współczynnik zmienności
![]()
![]()
interpretacja wyniku w procentach
Współczynnik zmienności informuje, jaki jest udział zmienności badanej cechy w odniesieniu do wartości przeciętnej analizowanej badanej cechy.
W przypadku rozkładu stałego (wszystkie obserwacje identyczne) przy braku zmienności wartości badanych cech miary zmienności wynoszą 0 (zero)
(~wariancja, odchylenie standardowe, współczynnik zmienności i odchylenie przeciętne)
Pozycyjne miary zmienności
- odchylenie ćwiartkowe (interkwarty)
współczynnik zmienności - miary pozycyjne
(~liczymy gdy nie można z innych powodów
zmierzyć miary asymetrii)
Miary symetrii Mediana
Dla rozkładu symetrycznego
x = D = Me
x - wartość średnia
D - dominanta mają tę samą wartość
Me - mediana
Badając asymetrię rozkładu cechy statystycznej należy określić:
ASYMETRIA
Miary asymetrii
Współczynnik skośności Persona
Jest wielkością niemianowaną o wartościach z przedziału od -1 do +1
Im większa wartość bezwzględna współczynnika skośności tym większa siła asymetrii
As [-1, 1]
0,3 słaba (od 0 do 3)
- 0,6 średnia
0,8 silna
Współczynnik asymetrii
Q dzieli obszar na jednakowe ćwiartki
klasyczna miara symetrii
[ ]3 jednostka kubiczna
M3 moment centralny
γ3 moment centralny zestandaryzowany
Analiza współzależności dwóch cech statystycznych
- należy ustalić typy powiązań
- pomiar
rodzaje zależności między dwoma zmiennymi
dwie badane cechy X (ocena z jednego języka) Y (ocena z drugiego języka)
ad a) zależność funkcyjna wraz ze zmianą wartości jednej zmiennej następuje ściśle określona zmiana wartości drugiej zmiennej (~do wyliczania podatków, oprocentowania obligacji)
ad. b) zależność sochastyczna wraz ze zmianą wartości jednej zmiennej następuje zmiana rozkładu prawdopodobieństwa drugiej zmiennej (~jak sprzedają się oferty turystyczne - nie przewidywalne)
ad. c) zależność korelacyjna: - liniowa, - nieliniowa wraz ze zmianą wartości jednej zmiennej następuje zmiana wartości średnich drugiej zmiennej ustaleniu typu zależności służy wykonanie wykresu: - rozrzutu, - diagram korelacyjny
rodzaje zależności korelacyjnej
Zależność korelacyjna liniowa dodatnia ma miejsce wówczas, gdy: wraz ze wzrostem wartości jednej cechy następuje wzrost wartości drugiej cechy
Zależność korelacyjna liniowa ujemna ma miejsce, gdy: wraz ze wzrostem wartości jednej cechy nastepuje spadek wartości drugiej cechy.
Pomiar siły zależności korelacyjnej - w przypadku zbieżności liniowej
Siłę zależności korelacyjnej wyznaczamy wykorzystując współczynnik korelacji liniowej Pearsona
cov - kowariancja jest to liczba niemianowana o wartościach unormowanych do przedziału od - do +1
Miernik jest symetryczny
Obroty dzienne (mln zł) |
10 |
12 |
14 |
15 |
17 |
18 |
19 |
21 |
22 |
23 |
Zapasy (mln zł) |
41 |
40 |
38 |
37 |
35 |
33 |
31 |
34 |
32 |
30 |
Zad. Zbadać zależność korelacyjną wielkości dziennych obrotów oraz wysokości zapasów w wybranych hurtowniach
2. Pomiar natężenia (wyznaczanie współczynnika korelacji)
3. odchylenie wartości badanych cech od wartości przeciętnych xi - x ,y - y
Obroty dzienne (mln zł) |
Zapasy (mln zł) |
|
|
|
|
|
10 |
41 |
-7,1 |
5,9 |
50,41 |
34,81 |
-41,89 |
12 |
40 |
-5,1 |
4,9 |
26,01 |
24,00 |
-24,99 |
14 |
38 |
-3,1 |
2,9 |
9,61 |
8,41 |
-8,99 |
15 |
37 |
-2,1 |
1,9 |
4,41 |
3,61 |
-3,99 |
17 |
35 |
-0,1 |
-0,1 |
0,01 |
0,00 |
0,01 |
18 |
33 |
0,9 |
-2,1 |
0,81 |
4,41 |
-1,89 |
19 |
31 |
1,9 |
-4,1 |
3,61 |
16,81 |
-7,79 |
21 |
34 |
3,9 |
-1,1 |
15,21 |
1,21 |
-4,29 |
22 |
32 |
4,9 |
-3,1 |
24,00 |
9,61 |
-15,19 |
23 |
30 |
5,9 |
-5,1 |
34,81 |
26,01 |
-30,09 |
171 |
351 |
x |
y |
168,90 |
128,9 |
-139,10 |
Wariancje badanych cech
Odchylenia standardowe badanych cech
Kowariancja
Współczynnik korelacji
Współczynnik determinacji informuje jaki procent zmian wartości cechy x (y) jest wyjaśniony zmianami wartości cechy x (y)
Dodatkowo wyznaczamy wartość współczynnika determinacji
W badanej próbie zachodzi silna ujemna liniowa zależność korelacyjna pomiędzy wielkością dziennych obrotów z wysokością zapasów, czyli, że wraz ze wzrostem wielkości obrotów maleje wielkość zapasów. Wielkość dziennych zapasów w 88,9% zależy od wysokości obrotów, natomiast w pozostałych od innych czynników.
14
Mamy 3 różne wartości i 7 obserwacji
![]()
36 obserwacji
ile wartości w badanej próbie
(nie określamy w przedziałach)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
10
8
6
4
2
ni
40
30
20
10
Liczba maszyn
![]()
xi
[czas w godz.]
Wielobok liczebności
(środki przedziału łączymy)
Krzywa liczebności
Mo
![]()
![]()
![]()
![]()
Me
Q3
Q2
Q1
50%
50%
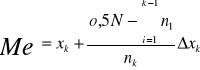
![]()
![]()
![]()
Próba 1
x1: 1, 2, 3, 4, 5
x = 3
x1- x
-2, -1, 0, 1, 2
Próba 2
x1: 2, 3, 3, 3, 4
x = 3
x1- x
-1, 0, 0, 0, 1
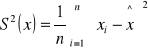
![]()
![]()
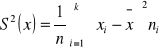
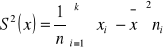
![]()
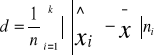
![]()
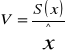
Próba 2
x1: 2, 3, 3, 3, 4
x = 3
x1- x : 0, 0, 0, 0, 0
S2(x) = 0
S(x) = 0
![]()
d=0
![]()
![]()
Krzywa liczebności
Częstość względna
x
50 %
50 %
Mediana
x
Częstość względna
x
x
Częstość względna
Częstość względna
![]()
![]()
dominanta
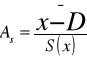
![]()
![]()
![]()
![]()
25 %
25 %
x
25 %
25 %
Q1
Q2
Q3
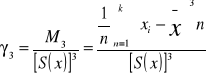
Zależność liniowa ujemna
Zależność nieliniowa
x
x
x
y
Zależność liniowa dodatnia
y
y
r bliskie zeru
Brak zależności
x
r>0
r<0
y
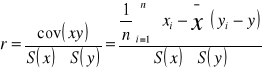
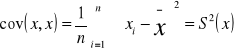
![]()
obwiednia
Zależność liniowa ujemna
40
20
10
20
obroty
10
30
40
30
zapasy
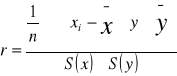
![]()
t i - czas
y i - cecha zmienna (ile?)
![]()
![]()
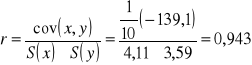
![]()
![]()
![]()
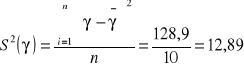
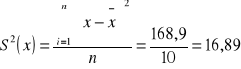
![]()
![]()
![]()