dr Anna Barbaszewska-Wiśniowska

FUNKCJE I ODWZOROWANIA

Zad.1. Zapisz za pomocą kwantyfikatorów i notacji logicznej podstawowe własności funkcji a następnie utwórz ich zaprzeczenia. Każdą własność zilustruj prostym przykładem.

Zad.2. Zbadaj parzystość (nieparzystość) funkcji

,
,
,
,
,

,
,

Zad.3. Naszkicuj wykresy

,
,
,
,
,
,

,
,
,

,
,

,
,

Zad.4. Niech

Wyznacz złożenia

Zad.5. Znajdź funkcje, z których są utworzone następujące funkcje złożone

,
,
,

Zad.6. Znajdź dziedziny naturalne funkcji

,
,
,

,
,

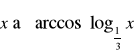
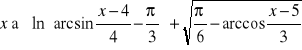
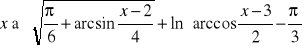
Zad.7. Omów ogólne własności złożeń funkcji wzajemnie odwrotnych i podaj odpowiednie wzory dla znanych funkcji elementarnych.

Zad.8. Zbadaj czy następujące funkcje są odwracalne, a jeżeli tak to znajdź dziedzinę, przeciwdziedzinę, podaj wzór na
oraz określ dziedzinę funkcji odwrotnej

gdzie x<0

Zad.9. Znajdź funkcje odwrotne do odpowiednio zawężonych funkcji:

a.

b.

c.

d.

Zad.10. Dobierz tak zbiory X oraz Y by

a. f było odwzorowaniem X w Y

b. f było odwzorowaniem X na Y

c. f było iniekcją

d. f było bijekcją

Zad.11. Oblicz

a.

b.

Zad.12. Naszkicuj wykresy
oraz

a.

b.

c.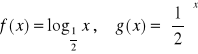

d.

Zad.13. Omów charakter monotoniczności funkcji wzajemnie odwrotnych oraz złożeń.

Zad.14. Wyznacz zbiory:

a.
gdzie

,

b.
gdzie

,

---