Akademia Techniczno- Humanistyczna

w Bielsku - Białej

Wydział Nauk o Materiałach i Środowisku

Kierunek: Ochrona Środowiska

Semestr II

SPRAWOZDANIE

TEMAT : BADANIE WPŁYWU TEMPERATURY NA OPORNOŚĆ ELEKTRYCZNĄ CIAŁ STAŁYCH.

ĆWICZENIE nr 56.

Wykonali:

Anna Dziergas

Barbara Fojcik

Marek Tittor

Wstęp teoretyczny.

Opór elektryczny przewodników w temperaturach dużo wyższych od temperatury Debye'a rośnie liniowo wraz ze wzrostem temperatury:

(1)

gdzie: R_o - opór elektryczny przewodnika w temp. otoczenia,

T - przyrost temperatury,

 - temperaturowy współczynnik oporności elektrycznej.

Dla przewodnika w tym zakresie temperatur opór elektryczny maleje ekspotencjalnie ze wzrostem temperatury:

(2)

gdzie: E - szerokość pasma wzbronionego,

k - stała Boltzmana,

R_po - stała oporności zależna od koncentracji nośników ładunku
w stopniu podstawowym i ich ruchliwości.

Logarytmując obustronnie równanie (2) otrzymujemy liniowe zależności lnR od odwrotności temperatury w skali bezwzględnej 1/T [K^-1]

(3)

Wyznaczając parametry prostej korelacji y=ax+b dopasowanej do eksperymentalnego wykresu funkcji:

1. R / R_o=f (T) (dla przewodnika) temperaturowy współczynnik oporności obliczyć można z wartości współczynnika kierunkowego tej prostej,

2. ln R=f (1/T) (dla półprzewodnika) szerokość pasma wzbronionego E dla badanego półprzewodnika obliczyć można z wartości współczynnika kierunkowego tej prostej. Jego wartość jest bowiem równa E/k. Wyraz stały prostej korelacji jest równy natomiast wartości ln R_po.

TABELA POMIAROWA:

Tab.1.

t [^oC]	przewodnik				półprzewodnik
		ΔT [C]	R1 [Ω]	ΔR1 [Ω]	R1/Ro	T [°K]	1/T 10^-4[1/K]	R2 [kΩ]	ΔR2 [kΩ]	lnR2
20	0.0	17.68	0.18	1.000	293.15	34.11	10.40	10.401	9.250
25	5.0	17.95	0.18	1.015	298.15	33.54	8.21	8.211	9.013
30	10.0	18.28	0.18	1.034	303.15	32.99	6.37	6.375	8.759
35	15.0	18.63	0.19	1.054	308.15	32.45	5.05	5.053	8.527
40	20.0	18.97	0.19	1.073	313.15	31.93	4.06	4.063	8.309
45	25.0	19.33	0.19	1.093	318.15	31.43	3.27	3.276	8.093
50	30.0	19.69	0.20	1.114	323.15	30.95	2.72	2.725	7.908
55	35.0	20.04	0.20	1.133	328.15	30.47	2.26	2.268	7.723
60	40.0	20.39	0.20	1.153	333.15	30.02	1.90	1.903	7.550
65	45.0	20.76	0.21	1.174	338.15	29.57	1.62	1.624	7.390
70	50.0	21.14	0.21	1.196	343.15	29.14	1.39	1.395	7.237
75	55.0	21.52	0.22	1.217	348.15	28.72	1.20	1.204	7.090
80	60.0	21.91	0.22	1.239	353.15	28.32	1.04	1.044	6.947

ΔR₁ = R_1n - R_1n-1 ; ΔR₂ = R_2n - R_2n-1 (n - numer kolejnego pomiaru)

Błąd odczytu rezystancji R dla przewodnika R=0,01*R

Błąd odczytu rezystancji R dla półprzewodnika R=0,0165*R

Wykorzystując metodę najmniejszych kwadratów obliczamy współczynniki kierunkowe prostych R/R_o=f (T) - dla przewodnika i lnR=f (1/T) dla półprzewodnika:

PRZEWODNIK: PÓŁPRZEWODNIK:

a = 4.0158E-03 b = 9.9460-01 a =3.9805E+03 b = -4.3751E+00

a = 3.6E-05 b = 1.3E-03 a=5.3E+01 b =1.6E-o.1

a= 0,004 [K^-1] a= 3999,605 [K]

a=0,0000736 a=56,96

Wartość pasma wzbronionego półprzewodnika obliczamy z zależności:

E=a  k

gdzie:

k - stała Boltzmana

a - współczynnik kierunkowy prostej lnR = f (1/T)

E= 3999,605 K  8,61734210^-5 eV/K = 0,34 eV

E=0,34 eV

ΔE=0,034 eV

E=0,34[eV] 0,034[eV]

Dla półprzewodnika:

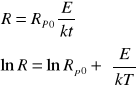
stąd wynika, że: b=lnR_p0

lnR_p0=-11,25 => R_p0=0,000013

Dla przewodnika:

R=R_p0(1+T), czyli =a

PRZEWODNIK		PÓŁPRZEWODNIK
R/Ro	[K^-1]	Rpo [k]	E/k [K]	E [eV]
1	0,004 0,0000736	0,000013	3999,6	0,34

WYKRESY:

6

---