Momentem siły P względem punktu 0 nazywamy iloczyn wektorowy tej siły przez promień - wektor łączący 0 z dowolnym punktem na linii działania tej siły.

Prawa tarcia Coulomba i Morena:

Siła tarcia nie zależy od wielkości stykających się powierzchni, a jedynie od ich rodzaju

Wielkość siły tarcia waha się od 0 do tzw. wartości granicznej T_g, która jest proporcjonalna do nacisku normalnego N cięzaru na podłogę.

W przypadku, gdy ciało ślizga się po pewnej powierzchni, siła tarcia jest skierowana zawsze przeciwnie do kierunku ruchu, wielkość jej zaś niie zależy w przybliżeniu od prędkości poślizgu

TARCIE KINETYCZNE

Q_GR=μG; T_MAX=μT; 0≤Q≤ Q_GR; 0≤T≤T_GR

tgϕ_gr= T_GR/N=μN/N=μ ; ϕ_gr=arctgμ ; 0≤ϕ≤ϕ_GR

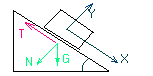
Tarcie na równi pochyłej

Suma P_X=0 Gsinα-T=0

Suma P_Y=0 N-Gcosα=0

T_MAX=μT; T_MAX= Gsinα_max; tgα_max=μ

α_max=arctgμ warunek samohamowalności równi

Tarcie przy toczeniu

QR=NT f- współ. tarcia przy toczeniu

Nf_Max=M_T moment tarcia przy toczeniu

0≤ M_T≤QR=Nf

M_o=Σ_a=1ⁿM_a - moment główny układu sił

S=Σ_k=1ⁿP_k - wektor główny układu sił

M₀₁=M_0­-r×s - wzór Bosma (moment siły S względem bieguna O gdzie r = OO₁)

M_O1•S= M_OS=k=const Iloczyn momentu głównego względem dowolnego punktu ciała i wektora głównego układu jest równy iloczynowi mom. gł. układu względem bieguna redukcji O i jest stały = k.

S jest pierwszym niezmiennikiem układu sił.

k - parametr układu jest drugim niezmiennikiem układu sił.
Warunki równowagi płaskiego układu sił M._O=0 S=0

Moment statyczny względem osi lub płaszczyzny przechodzącej przez środek ciężkości jest zawsze równy 0.

Moment statyczny nie zmieni się, jeżeli zamiast części układu wprowadzimy punkt materialny o masie równej masie danej części leżący w środku ciężkości tej części masy.

Ruch płaski - ruch, w którym wszystkie punkty ciała poruszają się w płaszczyznach równoległych do pewnej płaszczyzny zwanej płaszczyzną kierującą.

x_m= x_m(t) y_m= y_m(t) ϕ=ϕ(t)

x_a=x_m+ξcosϕ-ηsinϕ
y_a=y_m+ξsinϕ+ηcosϕ

Prędkość dowolnego punktu w ruchu płaskim jest sumą geometryczną prędkości ruchu postępowego i prędkości ruchu obrotowego dookoła obranego bieguna.

1. Polega na tym, że znane są równania ruchu punktu, należy określić siły, które ten ruch wywołują.

{pogrubiona czcionka to wektor}

r=r(t)

r=x(t)i+y(t)j+z(t)k

x"(t)=a_x

y"(t)=a_y

z"(t)=a_z

P_x(t)=mx"(t)

P_y(t)=my"(t)

P_z(t)=mz"(t)

|P|=

2. Polega na tym, że znane są siły działające na punkt materialny P, a szukane są wielkości x=x(t). y=y(t), z=z(t)

P=P(r,r',...,t)
P_x=P(x,y,z,...,t)
P_y=P(x,y,z,...,t)
P_z=P(x,y,z,...,t)

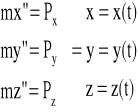
Zasada równoważności pracy i energii kinetycznej: Skończony przyrost energii kinetycznej układu mechanicznego ciał materialnych z położenia o konfiguracji elementów A do położenia o konfiguracji elementów B jest równy sumie prac całkowitych układów sił zewnętrznych i zewnętrznych na tym przemieszczeniu

mV_B²/2 - mV_A²/2 = L_AB ; E_kB - E_kA = L_AB

Przyrost E_k w czasie od t₁ do t₂ jest równy pracy wykonanej przez siłę działającą na punkt materialny w tym samym czasie.

Twierdzenie Steinera - moment bezwładności względem dowolnej osi jest równy momentowi osi równoległej i przechodzącej przez środek masy układu powiększonemu o iloczyn masy całkowitej i kwadratu odległości między tymi osiami. I = I₀ + md²

Twierdzenie Königa - energia kinetyczna ciała sztywnego równa się sumie energii kinetycznej ruchu postępowego całej masy skupionej w środku masy oraz energii kinetycznej ruchu obrotowego ciała sztywnego dookoła osi przechodzącej przez środek masy.

---