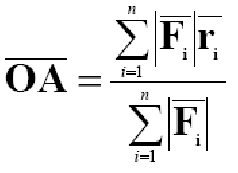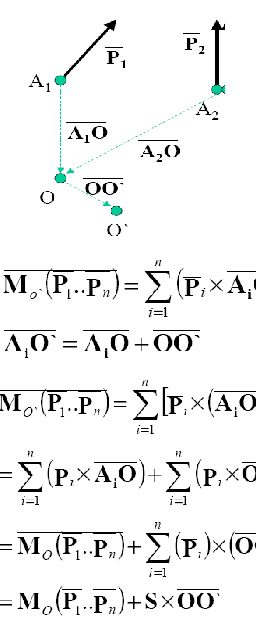
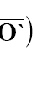

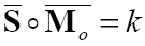
Iloczyn wektorowy:
prostopadłe, układ redukuje się do wypadkowej 1.Iloczyn wektorów równoległych jest zaczepionej w
wektorem zerowym
punkcie A tak dobranym by MA = 0 (punktu A poszukuje się
2. wektor f jest prostopadły do wektorów a i b korzystając z twierdzenia o zmianie bieguna) Iloczyn skalarny
Środek równoległego układu sił
- iloczyn skalarny wektorów prostopadłych Środek równoległego układu sił to punkt A wynosi zero
względem którego
Moment siły F zaczepionej w punkcie A moment układu wynosi 0
względem punktu B
(bieguna B)
M (F)=
×
= ×
Własności układów sił
Jeżeli do ciała przyłożone są dwie siły to równoważą się tylko wtedy
gdy mają wspólną prostą działania, te same Warunki równoważności układów sił
wartości i przeciwne
1.Dwa układy sił są sobie równoważne, jeżeli zwroty.
mają równe sobie sumy
Skutek działania dowolnego układu sił nie i momenty względem każdego punktu.
zmieni się gdy dodamy do
2.Dwa układy sił są równoważne, jeśli mają niego lub odejmiemy układ sił równoważących równe sumy i momenty
się.
względem dowolnego punktu (wystarczy Punkt przyłożenia siły można przesuwać względem jednego).
wzdłuż prostej jej działania.
3.Dwa układy sił są równoważne, jeśli mają Każdemu działaniu towarzyszy równe co do momenty względem 3
wartości, działające
różnych punktów nie leżących na jednej prostej wzdłuż tej samej prostej lecz mające przeciwny równe sobie.
zwrot
przeciwdziałanie.
Każde nieswobodne ciało można myślowo oswobodzić z więzów,
zastępując ich działanie reakcjami a następnie rozpatrywać jako ciało
swobodne pod działaniem sił czynnych (obciążeń) i biernych (reakcji)
Twierdzenie o zmianie bieguna Moment układu sił względem nowego bieguna Ò jest równy sumie momentu tego układu względem starego bieguna O i momentu sumy sił układu S (zaczepionej w punkcie O) względem nowego bieguna Ò
Wnioski wynikające z twierdzenia o zmianie bieguna
1.Jeżeli momenty układu sił względem 3
punktów nie lezących na jednej
prostej są sobie równe to suma układu jest wektorem zerowym.
2.Iloczyn skalarny
(parametr
układu k)względem dowolnego punktu jest wartością stałą i nie zależy od
wyboru bieguna
Zerowy układ sił – suma układu i moment względem dowolnego
punktu wynoszą zero
Para sił – dwie niezerowe siły przeciwne nie leżące na jednej prostej
Zbieżny układ sił – proste działania wszystkich sił przecinają się w jednym punkcie.
Płaski układ sił – wszystkie siły leżą w jednej płaszczyźnie.
Równoległy układ sił – wszystkie siły są równoległe do pewnej prostej
Redukcja układu sił – przypadki 1) k< >0, M< >0, S< >0 Można tak dobrać biegun redukcji O by
wektory S i MO były równoległe – redukcja do skrętnika
2) k=0
2a) S < > 0, MO=0 Układ redukuje się do wypadkowej, czyli wektora
sumy zaczepionego w punkcie O
2b) S = 0, MO< >0 Układ redukuje się do pary sił
2c) S = 0, MO = 0 zerowy układ sił
2d) S < > 0, MO < > 0 wektory sumy i momentu są do siebie
Wyszukiwarka
Podobne podstrony:
Iloczyn wektorowy i biegun
iloczyn skalarny iloczyn wektorowy
Cwiczenia iloczyn wektorowy
Cwiczenia iloczyn wektorowy
Inne materiały, man-twierdzenie sin i cos oraz iloczyn wektorów, a/sinα=b/sinβ=c/sinγ=2R - tw
scg, Momentem siły P względem punktu 0 nazywamy iloczyn wektorowy tej siły przez promień - wektor łą
Iloczyn wektorowy
Gradient dywergencja rotacja operatorNabla iloczyn wektorowyIskalarny Wiki, Politechnika Poznańska,
Iloczyny wektorow id 210761 Nieznany
21 Iloczyn wektorowy
Iloczyn mieszany wektorów
Iloczyn skalarny wektorowy
matematyka, iloczyn, Iloczyn skalarny wektorów
fiz-indukcja elektromagnetyczna, Strumień indukcji magnetycznej - jest równy iloczynowi skalarnemu w
Matematyka I (Ćw) Lista 06 Wektory Iloczyn skalarny, wektorowy, mieszany
matematyka, Iloczyn skalarny, Iloczyn skalarny wektorów
więcej podobnych podstron