Testowanie Hipotezy Na Jednej Populacji

1. Określamy rozkład np. X~N (μ, δ²) lub X€<0,1> (p, n)

2. Stawiamy hipotezę: H₀ i H₁ np. H₀ μ=23; H₁ μ ≠23

3. Wybieramy Funkcję testową (np. test t-studenta; test F)

4. Porównujemy wartości t_emp i t_kryt

t_kryt= α; V gdzie V=n-1 (wartość ta odczytujemy z tablicy t-studenta)

t_emp - odczytujemy ze Stargraphics'a ( Computed t statistic = t_emp)

Jeśli t_emp ≥ t_kryt to H₀ odrzucamy

5. Formułujemy wniosek statystyczny (Hipotezy zerowej nie można odrzucić / Hipotezę zerową odrzucamy)

6. Formułujemy wniosek merytoryczny

Zadanie przykładowe

X - zawartość witaminy C w konserwowym soku pomidorowym

X~N (μ, δ²)

H₀ μ=23; H₁ μ ≠23 n=17

Funkcja testowa t-studenta

Sposób I

t_emp= - 4,98

t_kryt(α; V) t_kryt (0,05; 16) = 2,1199

t_kryt > t_emp

Wniosek statystyczny: Hipotezę zerową odrzucamy

Wniosek merytoryczny: Niemożna przyjąć, że średnia zaw. Witaminy C wynosi 23

Sposób I

Stargraphics

Describe -› Distributions -› Propability Distribution

Prawy przycisk -› Analisis Opions (wpisujemy wartość n-1) -› Tabular -› Inverse CDF

Tabula -› Hypothesix test

P-Value - odczytujemy ze Stargraphics'a

Jeśli P-Value < α to H₀ odrzucamy

0,00013 < 0,05

Rejent Null Hypothesis = Hipotezę zerową należy odrzucić (Stargraphics)

Zadanie

a) Producent twierdzi, że zawartość witaminy C w konserwowym soku pomidorowym wynosi 21/100mg

X - zawartość witaminy C w konserwowym soku pomidorowym

X~N (μ, δ²)

H₀ μ=21; H₁ μ≠21 n=17

Funkcja testowa t-studenta

Describe -› Hypothesix test -› Normal mean (Null Hypothesis = Hipoteza zerowa; Simple size = ilość prób)

Odczytujemy wartość Computed t statistic (t_emp) i porównujemy z t_kryt odczytane z tablicy (t_kryt(α; V) = t_kryt (0,05; 16))

Jeśli t_emp ≥ t_kryt to H₀ odrzucamy

LUB

Odczytujemy wartość P-Value I porównujemy ze stopniem zgodność α.

Jeśli P-Value < α to H₀ odrzucamy

Wyrażenie „Rejent Null Hypothesis” oznacza, że Hipotezę zerową należy odrzucić

Wniosek statystyczny: Hipotezę zerową odrzucamy

Wniosek merytoryczny: Niemożna przyjąć, że średnia zaw. Witaminy C wynosi 21. Odrzucamy założenie producenta

b) ) Producent twierdzi, że zawartość witaminy C w konserwowym soku pomidorowym przekracza 21/100mg

X - zawartość witaminy C w konserwowym soku pomidorowym

X~N (μ, δ²)

H₀ μ=21; H₁ μ>21 n=17

Funkcja testowa t-studenta

Describe -› Hypothesix test -› Normal mean (Null Hypothesis = Hipoteza zerowa; Simple size = ilość prób)

Prawy przycisk -Amalisis options (zmieniamy na Greater than)

Odczytujemy wartość Computed t statistic (t_emp) i porównujemy z t_kryt odczytane z tablicy (t_kryt(α; V) = t_kryt (0,05; 16))

Jeśli t_emp ≥ t_kryt to H₀ odrzucamy

LUB

Odczytujemy wartość P-Value I porównujemy ze stopniem zgodność α.

Jeśli P-Value < α to H₀ odrzucamy

Wniosek statystyczny: Hipotezy zerowej nie można odrzucić

Wniosek merytoryczny: Średnia zaw. Witaminy C może wynosić 21. Odrzucamy założenie producenta

c) Towarzystwo konsumenckie uważa, że zawartość witaminy C w konserwowym soku pomidorowym nie przekracza 21/100mg

X - zawartość witaminy C w konserwowym soku pomidorowym

X~N (μ, δ²)

H₀ μ=21; H₁ μ<21 n=17

Funkcja testowa t-studenta

Describe -› Hypothesix test -› Normal mean (Null Hypothesis = Hipoteza zerowa; Simple size = ilość prób)

Prawy przycisk -Amalisis options (zmieniamy na Less than)

Odczytujemy wartość Computed t statistic (t_emp) i porównujemy z t_kryt odczytane z tablicy (t_kryt(α; V) = t_kryt (0,05; 16))

Jeśli t_emp ≥ t_kryt to H₀ odrzucamy

LUB

Odczytujemy wartość P-Value I porównujemy ze stopniem zgodność α.

Jeśli P-Value < α to H₀ odrzucamy

Wniosek statystyczny: Hipotezę zerową odrzucamy

Wniosek merytoryczny: Średnia zaw. Witaminy C nie może wynosić 21. Przyjmujemy założenie Towarzystwa konsumenckiego

Zadanie

Czy na podstawie badanej próby można stwierdzić, że siła kiełkowania ziaren badanej odmiany grochu wynosi 90%

n = 800 wykiełkowało = 728

X€<0,1> (p, n) => p - prawdopodobieństwo; n - liczebność

H₀ p=0,9 H₁ p≠0,9

Describe -› Hypothesis -› Binomial Propotion - uzupełniamy dane: Null Hypothesis = 0,9

Sample propation = 728 / 800= 0,91

Simple size = 800

Odczytujemy otrzymane wyniki

Wniosek: …….

Testowanie Hipotezy Na dwie Populacje

Zadanie

20 wazonów z pszenicą = 10 nawożonych + 10 nie nawożonych

Czy nawóz wpływa na plonowanie danej odmiany? (α=0,05 oraz α=0,01)

X₁ - plonowanie pszenicy nawożonej

X₂ - plonowanie pszenicy nie nawożonej

X₁~N (μ₁, δ₁²)

X₂~N (μ₂, δ₂²)

H₀ μ₁ = μ₂ H₁ μ₁ ≠ μ₂

Funkcja testowa t-studenta

Weryfikacja hipotezy:

Stargraphics

Compare → Two Simples → Two Simples Comperison → Tabular Options → Comparison of mean

Odczytujemy dane:

Wartość funkcji testowej → t = 4,43

P - Value = 0,00032

α = 0,05

Wniosek statystyczny: H₀ odrzucamy przy poziomie istotności 0,05

Wniosek merytoryczny: Możemy stwierdzić, że nawożenie wpływa na plon pszenicy…

Przy założeniu

H₀ δ₁² = δ₂² H₁ δ₁² ≠ δ₂²

Compare → Two Simples → Two Simples Comperison → Tabular Options → standart devation

Założenie zostało spełnione.

Analiza Wariacji

Badana cecha → X

Poziom czynnika → X₁

Czynnik X₁ → nawożenie w ”i”-tej dawce

i = 1, 2, 3, 4, 5

Zadanie

Badana cecha → X = plon pszenicy

X₁ → plon pszenicy w ”i”-tej odmianie

i = 1, 2, 3, 4, 5

n = 4 (4 poletka = 4 powtórzenia)

H₀ μ₁ = μ₂ = μ₃ = μ₄ = μ₅

Metoda weryfikacji: Analiza wariancji

Stargraphics

Col 1 → plony każdej odmiany

Col 2 → odmiana (1, 2, 3…)

Comper → Analisis of Variance → One-way ANOWA

Tabular → Anowa Table

Source (Źródło zmienności)	Sum of Squaras Suma kwadratów	Df Stopień swobody	Mean Square Średnia Kwadratów	F-Ratio Fempiryczne	P-Value
Between groups Czynnik (odmiana)	0,15 (SSA)	a-1 = 4 a = czynnik = 5	SSA / DfA	11,51	0,002
Within groups Błąd statystyczny	0,05 (SSE)	N-1 = 19 N = n *a = 5*4=20	SSE / DfE
Total całkowita

Wniosek statystyczny: H₀ odrzucamy

Wniosek Merytoryczny: Stwierdzono statystycznie zróżnicowanie na wartości plonów pszenicy

Czy, które odmiany plonują na tym samym poziomie?

Tabula → Multiple Range Test

Interpretacja danych:

Tabela pierwsza:

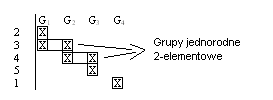
G₁→ podobne plony

G₂→ podobne plony

G₃→ podobne plony

Tabela druga

Contrast	Difference	+/- Limitees (NIR)
1-2	+ 0,2475	0,08
1-3	+ 0, 0925	0,08
1-4	…	0,08
…	…	…

Procedura Tukey

NIR^T = 0,08 NIR^T < Pif (z Kontrast np. 1-3)

Wyniki:

NIR^T = 0,08

Tab I

Grupy jednorodne:

Odmiany 2 i 4 są jednorodne, różnica między nimi wynosi….

2