Badanie nośności pali, nośność pali, nośność graniczna

analiza krzywej Q-S, krzywa obciążenie osiadanie

Grzegorz SZMECHEL

mgr inż. Zachodniopomorski Uniwersytet Technologiczny w Szczecinie

UPROSZCZONA METODA INTERPRETACJI TESTÓW

STATYCZNYCH PALI NA PODSTAWIE BADAŃ TERENOWYCH

STRESZCZENIE: W pracy przedstawiono interpretację krzywych obciążenie osiadanie uzyskanych ze

statycznych obciążeń próbnych pali w zakresie ograniczonych obciążeń. Podstawowym problemem w

wymiarowaniu pali, jest określenie nośności granicznej na podstawie danych z testów statycznych, które

obejmują jedynie początek krzywej Q-S. Założenia podstawowe opierają się na liniowej teorii Boussinesqa.

Rozwinięcie w logarytm naturalny równania uzyskanego z poprzednich rozważań pozwala sformułować

nową zależność dającą dobrą zgodność wyników terenowych obciążeń i ich aproksymacji. Dodatkowo

uproszczona metoda pozwala określić nośność graniczna pala z dostateczną dla celów inżynierskich

dokładnością. W dalszych badaniach planuje się rozwinięcie równania tak, aby możliwe było określenie nie

tylko przebiegu krzywej, nośności granicznej, ale i przybliżonych wartości parametrów gruntowych w

otoczeniu pala.

WSTĘP:

Rosnące zapotrzebowanie na nowe tereny inwestycyjne, oraz chęć wznoszenia coraz większych obiektów

sprawiają, iż w praktyce inżynierskiej wykorzystanie posadowienia na palach nabiera coraz większego

znaczenia. Obecnie stały się one jedną z najbardziej popularnych form posadowienia obiektów przenoszących na

podłoże znaczne obciążenia, szczególnie w trudnych warunkach gruntowych. Wobec tego pojawia się problem

optymalizacji nośności pali. Jednym z możliwych podejść jest projektowanie pali w oparciu o wyniki testów

statycznych, czyli z zachowaniem warunków najbardziej zbliżonych do rzeczywistego zachowania pala w

gruncie. Badania te maja na celu określenie nośności pala, wielkości osiadań, potwierdzenia prawidłowości

zaprojektowanego rozwiązania. Często jesteśmy także zainteresowani określeniem granicznej nośności pala N

gr

,

ponieważ to właśnie nośność graniczna określa zapas bezpieczeństwa. W praktyce stan nośności granicznej

podczas badań statycznych jest rzadko osiągany, z uwagi na bardzo duże siły, jakie należałoby w tym celu

przyłożyć na pal. Jako efekt obciążeń statycznych pala otrzymujemy krzywą obciążenie osiadanie, czyli krzywą

Q-S.

W celu określenia całego przebiegu krzywej Q-S, a co za tym idzie nośności granicznej pala, w literaturze

znaleźć można wzory pozwalające w sposób przybliżony określić jej przebieg. Ocena analityczna krzywej Q-S

jest zagadnieniem złożonym z uwagi na wiele czynników warunkujących pracę pala, w tym min. układ warstw

geotechnicznych, występowanie naprzemienne gruntów spoistych i niespoistych, technologię wykonywania pali,

sztywność fundamentu i układ grupy palowej to tylko niektóre z ważnych czynników mających wpływ na

przebieg krzywej osiadania. W literaturze znaleźć można wiele metod analitycznego określenia krzywej

obciążenie osiadanie. [1,3,4,5,7,8]

Dotychczas dla pala pojedynczego najczęściej stosowano metody w dużej mierze bazujące na teorii

sprężystości, w tym teorii Mindlina [5], oraz metody bazujące na wykorzystaniu funkcji transformacyjnych

[4,5,6]. Coraz częściej do takiej analizy wykorzystuje się badania ”In situ” sondowań CPT, CPTU itp. W dobie

rozwiniętej technologii komputerowej należy także wspomnieć o rozwiązaniach opartych o metodę elementów

skończonych i brzegowych MES i MEB [3]. Z punktu widzenia niniejszej pracy interesujące są rozwiązania

bazujące na wzorach empirycznych i pół empirycznych opartych na pomiarach z badań terenowych. Celem

pracy jest opracowanie metody, która szybko i z dostateczną dla celów inżynierskich dokładnością pozwoli na

prognozowanie przebiegu krzywej. Metodą taką jest aproksymacja przedstawiona przez Kowalowa-Meyera w

[8]. Równanie to zmodyfikowano poszukując możliwości wykorzystania analizy wstecznej do wyznaczenia

parametrów gruntowych.

1. KRZYWA APROKSYMACYJNA

Wg literatury krzywa aproksymacyjna testów statycznych zaproponowana przez Kowalowa i Meyera

powinna spełniać następujące warunki brzegowe:[9,10]

−

Dla N→0 krzywa S(N) dąży do linii prostej (asymptota ukośna)

−

Dla N→N

gr

osiadanie S powinno dążyć do nieskończoności, czyli mamy tu do czynienia z asymptotą

pionową

∞

Dla tak przyjętych warunków funkcję aproksymującą można przyjąć, jako:

(1)

gdzie:

A- stała [m]

κ- bezwymiarowy wykładnik potęgi

N- siła przyłożona w głowicy [kN]

N

gr

- graniczne obciążenie pala [kN]

Wygodniej natomiast jest operować pochodną funkcji S(N) dla N→0 jako pochodną:

!

" #

(2)

Stąd stała A jest równa:

# $

%

&

(3)

Podstawiając zależność (3) do wzoru (1) otrzymujemy:

#

%

%

"

(4)

Jest to podstawowa krzywa aproksymująca wyniki testów statycznych. Wprowadzenie stałej C wynika z

przyszłych zamiarów wykorzystania jej w opisie zjawiska liniowej teorii Bousinessqa. W oparciu o powyższe

założenia opracowano metodę parametryzacji funkcji S(N)[10]

Z badań terenowych mamy krzywa Q-S. Czyli ciąg wartości (Q

i

; S

i

). Chcielibyśmy przy pomocy tego zbioru

wartości aproksymować parametry stałe.

Praktyczne obliczenia wskazują iż wartość parametru

κ

jest niewielka, rzędu

κ

=0,1[10] . W pierwszej z

metod przyjmijmy zatem że

κ

→ 0. Otrzymamy wówczas rozwiązanie graniczne

%

'!

Dla wygody możemy napisać że:

'!

(

%

(5)

Dla założonych małych wartości

κ

- równanie (8) można przedstawić jako:

'!

)

(*+,-(

.

%

%/0

1

-

2

%

2

/0

2

%

(6)

'! 34

5

6

!34

6

(7)

%

'! 34

'

7

(8)

Oznacza to że dla małych wartości

κ

- oraz odpowiednio dobranego stosunku siły do nośności granicznej,

można wykorzystać tą funkcję jako przybliżoną metodę wyznaczenia krzywej Q-S.

#

89

34

(9)

Jest to krzywa:

%

'

7

#

89

'

7

(10)

gdzie:

#

:;<

=

=

>

-

=

?

:;

=

>

-

=

?

2

#;!@

89

?

(11)

Aby sprawdzić jak układają się krzywe dla poszczególnych wartości

κ

oraz N/N

gr

sporządzono tabelę dla

funkcji

' !A

oraz '

7

Tabela 1. Przebieg krzywej Q-S w zależności od wielkości współczynnika

κ

κ

f*

N/Ngr

0,01

0,05

0,10

0,15

0,3

0,357

0,360

0,363

0,366

0,357

0,4

0,512

0,517

0,524

0,530

0,511

0,5

0,696

0,705

0,717

0,729

0,693

0,6

0,920

0,937

0,958

0,979

0,916

0,7

1,211

1,240

1,276

1,313

1,204

0,8

1,622

1,674

1,739

1,804

1,609

Zachowanie krzywej Q-S w zależności od wartości współczynnika

κ

pokazuje wykres nr 1. Wynika z niego

iż wszystkie krzywe znajdują się w bliskim sąsiedztwie, ponad to rozwiązanie z

κ

=0 jest rozwiązaniem

granicznym, dającym dobrą zgodność z wynikami uzyskanymi z testów statycznych.

Rys 1. Wyniki osiadania pomierzone w wyniku testów statycznych na tle krzywej określonej analitycznie. N

gr

=4700 kN,

κ

=0,0-0,4

W sposób uproszczony spróbujmy oszacować N

gr

B

C

6

:;

D

CEF/

?

6

: G

D

#

C

H

I

6

(12)

JK

L

2

JM

N :

D

#

C

H

H

" O

(13)

JK

L

2

J

N : P

D

#

C

H

-

Q O

(14)

0,00

20,00

40,00

60,00

80,00

100,00

0

1000

2000

3000

4000

5000

Wartości Pomierzone

kappa =0

kappa =0,1

kappa=0,2

kappa=0,3

kappa=0,4

[mm]

[kN]

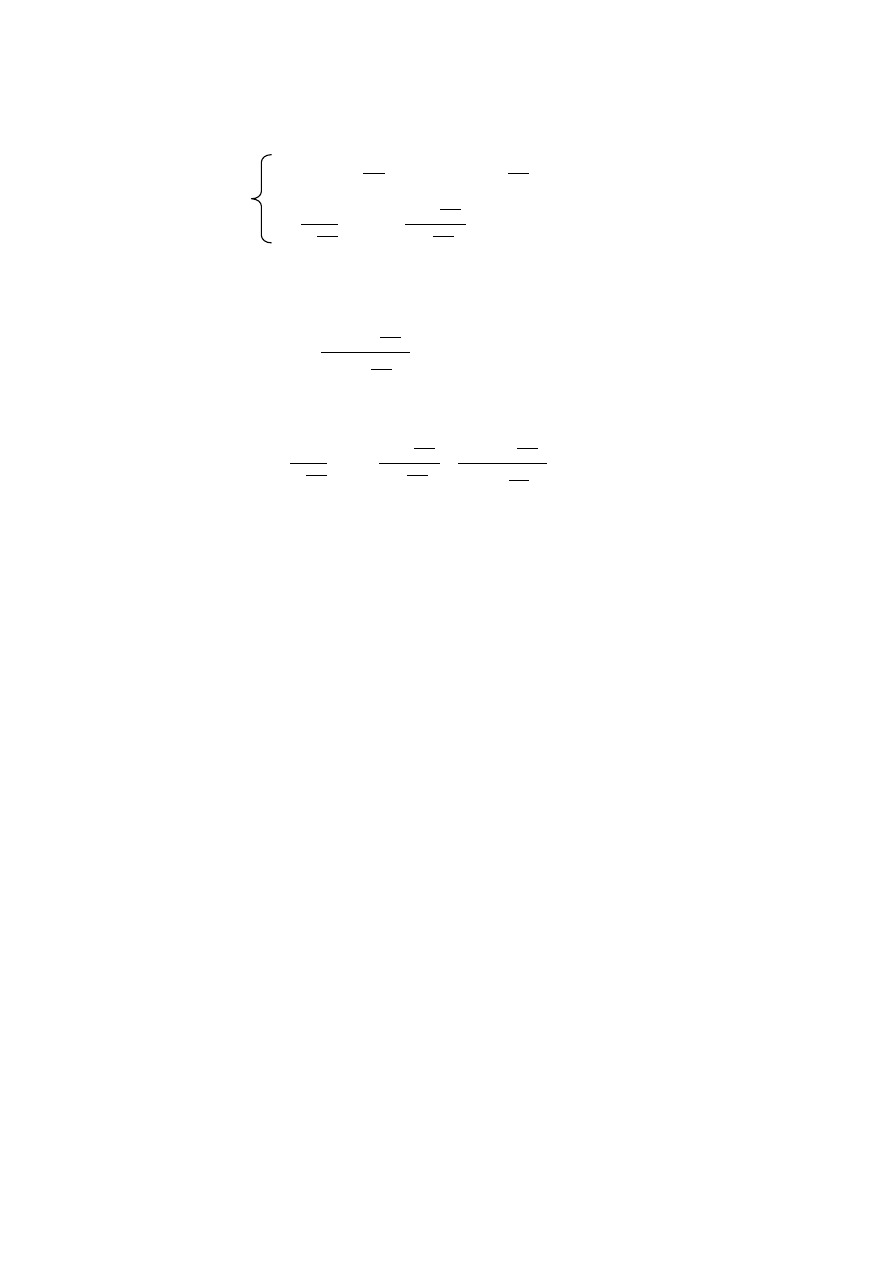
Otrzymujemy 2 równania:

:

D

H

" #

C

: H

"

6

O

(15)

: R

<

=

S #

C

: P

TU

Q O

(16)

Z układu równań 15 i 16 otrzymujemy N

gr

, tj. równanie warunkowe ma postać:

: <

=

TU

"

: TU

"

2

VW4X

(17)

I dalej:

: R

<

=

S : P

TU

Q

: <

=

TU

"

: TU

"

2

VW4X

(18)

Kolejnym krokiem jest iteracyjny dobór wartości N

gr

tak aby prawa strona równania była równa lewej.

Stosujemy wzór, (12) aby uzyskać rozwiązanie elementarne. A podstawowy warunek, czyli minimum sum

odchyłek kwadratów został spełniony z dostateczną dla celów inżynierskich dokładnością.

2. PRZYKŁAD OBLICZENIOWY

Zachowanie krzywej Q-S aproksymowanej z obliczeń porównano z wynikami statycznych obciążeń 6 pali

wykonanych na terenie Szczecina przez autora pracy. Były to pale żelbetowe prefabrykowane o przekroju 40x

40 cm. Zostały zabite, jako pale kozłowe o nachyleniu 1: 4, długość wszystkich pali wynosiła od 22 dla sekcji 9-

17 do 26 m dla sekcji 1-3 [2].

Warunki gruntowe określono na podstawie profili wykonanych w bezpośrednim sąsiedztwie analizowanego

terenu.

Na podstawie przeprowadzonych badań polowych można stwierdzić, że w podłożu rozpatrywanego obiektu

występują holoceńskie i plejstoceńskie utwory czwartorzędowe.

Grunty rodzime przykryte są warstwą nasypów niekontrolowanych powstałych w wyniku uzdatniania terenu.

Są to przeważnie nasypy piaszczyste z domieszką cegły, betonu, żwiru i kamieni o miąższości około 2,0 m.

Poniżej nasypów nawiercono utwory akumulacji bagiennej i zastoiskowej – torfy i namuły, których miąższość

dochodzi do około 4,5 m. Poniżej utworów organicznych zalega stosunkowo duża seria osadów rzecznych-

fluwialnych: wykształcona głównie, jako piaski drobne w stanie luźnym oraz średniozagęszczonym.

Najstarszymi osadami stwierdzonymi w podłożu są utwory wodnolodowcowe, których strop nawiercono na

głębokości około 11,0 m. Są to piaski drobne, lokalnie piaski grube w stanie średnio zagęszczonym i

zgęszczonym. W warstwie tej posadowiono podstawy projektowanych pali prefabrykowanych. Schematycznie

warunki geotechniczne dla sekcji pokazano na rysunku. [2]

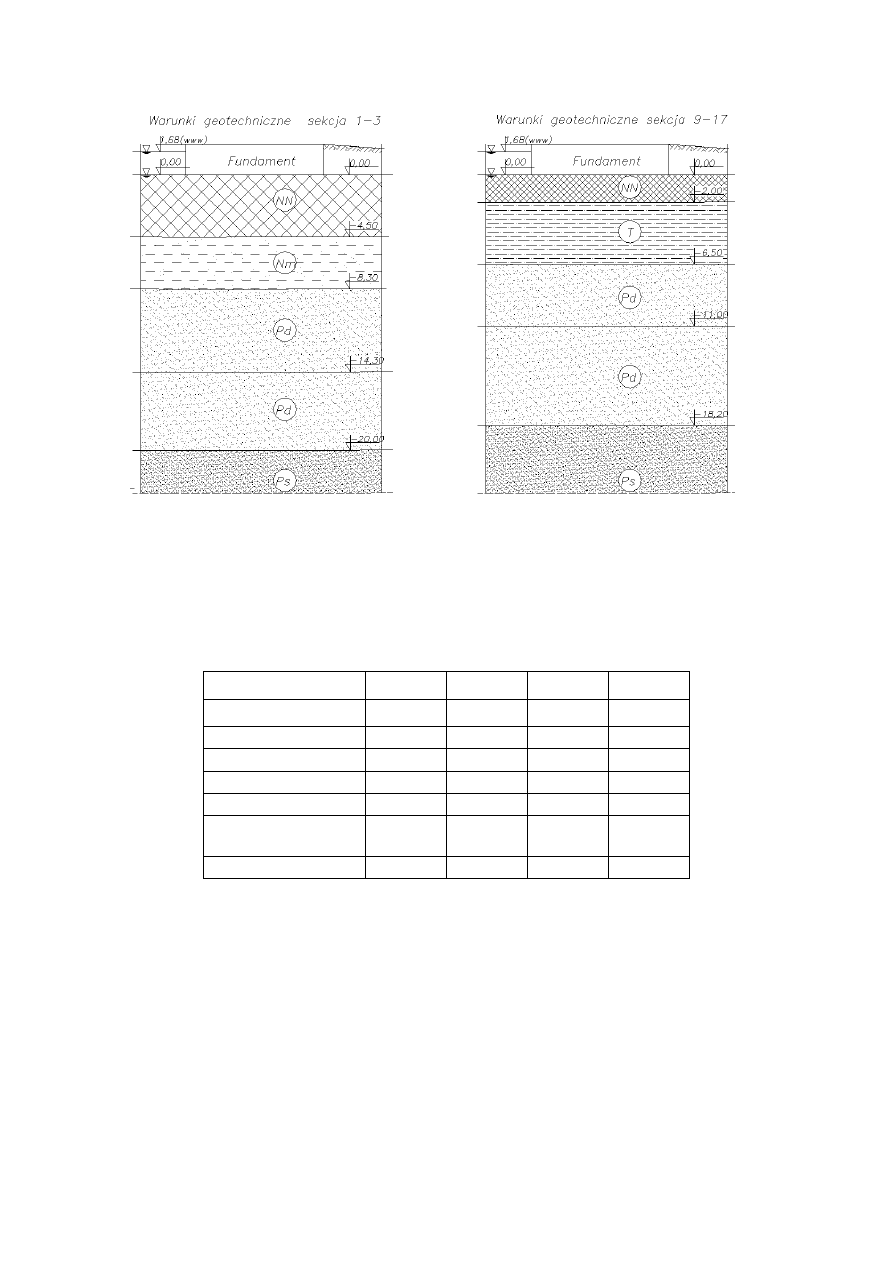
Rys 2. Warunki geotechniczne w rejonie prowadzenia badań.

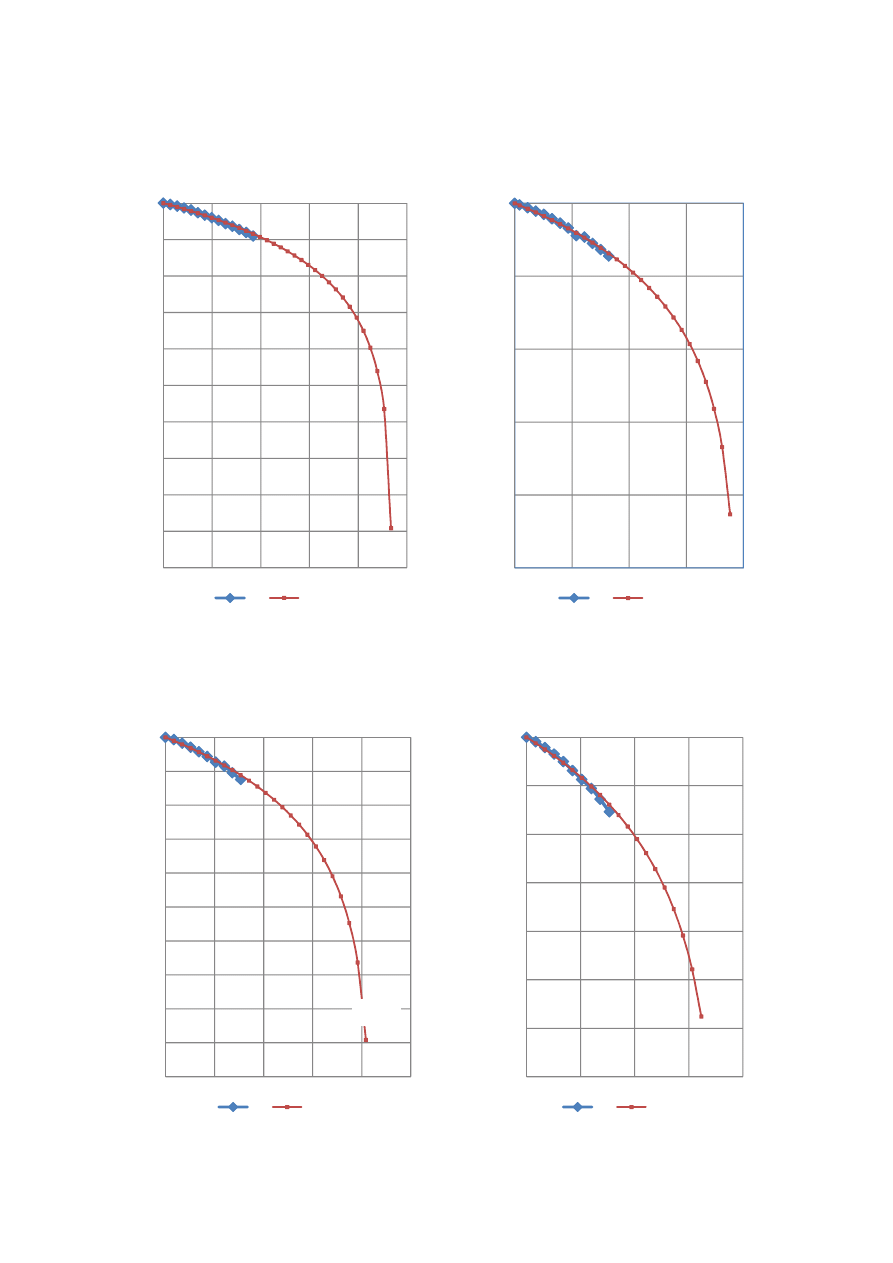
Wyniki analizy pracy pali przedstawiono w tablicy drugiej, wykresy 1–4 ilustrują przebieg krzywych

doświadczalnych zestawiony z przebiegiem krzywych teoretycznych.

Tablica 2. Wyniki analizy

Nr pala

x2

x8

x6

x06

Sekcja

1-3

1-3

9-17

9-17

S

max

[mm]

3,61

4,51

2,48

3,07

C [mm/kN]

0,00161

0,00179

0,00117

0,00139

R- współczynnik korelacji

0,998

0,999

0,998

0,998

N

gr

[kN]

3900

4700

4195

3590

k*Nc [kN] wg PN-83/B

02482

1315

1474

1225

1225

k·N

c

/N

gr

0,337

0,313

0,292

0,341

Z analizy wynika, iż przy zastosowaniu uproszczonej metody logarytmu naturalnego istnieje możliwość

analitycznego określenia krzywej obciążenie osiadanie oraz określenie Nośności granicznej pala, która wraz z

zapasem bezpieczeństwa na poziomie 70% pozwala oszacować normową wartość k·N

c

[11]. Analiza ta wymaga

dalszych badań na większym zbiorze danych wejściowych jednakże dotychczasowe wyniki badań potwierdzają

te założenia.

0,0

5,0

10,0

15,0

20,0

25,0

0

1000

2000

3000

4000

Krzywa Q-S. Obiekt Dźwig nabrzeżowy

szyna zewnętrzna Pal x8

Si

Si obl

0,0

2,0

4,0

6,0

8,0

10,0

12,0

14,0

16,0

18,0

20,0

0

1000

2000

3000

4000

5000

Krzywa Q-S . Obiekt Dźwig nabrzeżowy

szyna zewnętrzna Pal x6

Si

Si obl

0,00

2,00

4,00

6,00

8,00

10,00

12,00

14,00

0

1000

2000

3000

4000

Krzywa Q-S . Obiekt Dźwig

nabrzeżowy szyna zewnętrzna Pal x06

Si

S obl

Rys 3. Wykresy zależności, Q-S dla przykładowych pali.

0,0

5,0

10,0

15,0

20,0

25,0

30,0

35,0

40,0

45,0

50,0

0

1000

2000

3000

4000

5000

Krzywa Q-S. Obiekt Dźwig nabrzeżowy

szyna zewnętrzna Pal x2

Si

Si obl

R=0,999

R=0,998

[mm]

[kN]

[mm]

[kN]

[kN]

R=0,998

R=0,998

[mm]

[mm]

[mm]

[mm]

[kN]

3. PODSUMOWANIE I WNIOSKI:

1. W pracy przedstawiono metodę aproksymacji krzywej Q-S otrzymanej ze statycznych testów pali w oparciu o

zależności podane w literaturze [3,9,10]. W celu uzyskania większej dokładności obliczeń oraz przyspieszenia

procedury zastosowano rozwinięcie funkcji S w logarytm naturalny.

2. Uzyskane podczas symulacji wyniki wskazują, iż przedstawiona metoda analitycznej aproksymacji krzywej

obciążenie osiadanie w gruntach sypkich pozwala z dużą dokładnością aproksymować krzywą Q-S z

wykorzystaniem powyższej metody.

3. Uzyskane wartości k·N

c

[11] nośności granicznej odpowiadają wartością oczekiwanym od 0,29 do 0,34 wartości

N

gr

uzyskanej z rozważań teoretycznych. N

gr

uzyskana na podstawie analizy wynosi od 3590 kN do 4700 kN. Co

stanowi dostateczny zapas bezpieczeństwa.

4. Uzyskanie analitycznego związku obciążenie osiadanie oraz wartości N

gr

pozwala na weryfikację projektu

posadowienia i ewentualne korekty.

5. Problemem, który wymaga dalszej analizy jest ocena możliwości określenia parametrów gruntowych (zwłaszcza

modułów ściśliwości) z wykorzystaniem stałej C, która odpowiada poszczególnym krzywym obciążenia dla

bardzo małych obciążeń. Zakłada się, że w pierwszej fazie pracy dla bardzo małych obciążeń można przyjąć

liniową teorię Boussinesqa. Zależność tę można wykorzystać i zbudować stosowne zależności, które pozwolą

rozwiązać zadanie odwrotne, jakim jest określenie modułów ściśliwości. Zagadnienie to będzie przedmiotem

dalszych badań.

6. Innym problemem jest zbadanie czy istnieje zależność modułu ściśliwości gruntu od obciążenia granicznego.

Problem ten będzie również przedmiotem dalszych badań.

LITERATURA:

1. Bengt. H. Fellenius: What capacity value to choose from the results of static load test.

2. Gwizdała K., Słabek A., Szmechel G.: Ocena nośności pali prefabrykowanych 40 x 40 wykonanych pod posadowienie

samodzielnego fundamentu szyny poddźwigowej.

3. Bzówka J. Współpraca kolumn wykonywanych techniką iniekcji strumieniowej z podłożem gruntowym. Wydawnictwo

Politechniki Śląskiej. Gliwice, 2009

4. Cichy L., Rybak J., Tkaczyński G.: Badanie nośności pali prefabrykowanych. Nowoczesne Budownictwo Inżynieryjne,

2009

5. Gwizdała K., Fundamenty palowe. Tom 1, PWN 2010

6. Gwizdała K.: Kontrola nośności pali i jakości robót palowych. Geoinżynieria i Tunelowanie Nr 01/2004

7. Gwizdała K., Dyka I.: Analityczna metoda określania krzywej osiadania pala pojedynczego. Inżynieria i Budownictwo nr

12/2001

8. Meyer Z: Analiza Naprężeń na pobocznicy oraz pod podstawę pojedynczego pala w oparciu o liniową teorię Boussinesqa.

XVIII Seminarium Naukowe z cyklu Regionalne problemy inżynierii środowiska. 25.06.2010r

9. Meyer Z., Kowalów M.: Model Krzywej Aproksymującej wyniki testów statycznych pali. Inżynieria Morska i Geotechnika

Nr 3/2010

10. Meyer Z., Szmechel G.: Analiza możliwości analitycznej aproksymacji krzywej obciążenie osiadanie dla testów statycznych

pali żelbetowych w gruntach sypkich. Inżynieria Morska i Geotechnika Nr 4/2010

11. Norma Palowa PN-B-02482:1983

12. Bronsztejn I, Siemiendiajew K: Matematyka Poradnik Encyklopedyczny. PWN Warszawa 2010 Wydanie XX.