Laboratorium urządzeń

nadprzewodnikowych

Projekt elektromagnesu nadprzewodnikowego

Grupa ED 5.1

Paweł Mazurek

Paweł Pławski

Jacek Maliszewki

1.Cel projektu.

Na podstawie poniższych założeń zaprojektowane zostały cewki z nadprzewodników Nb₃Sn i NbTi oraz elektromagnes dwusekcyjny z nadprzewodników Nb₃Sn i NbTi.

2. Założenia.

indukcja w centrum elektromagnesu - B₀=8.5T

promień wewnętrzny pierwszej cewki - a₁=0.15m.

temperatura pracy uzwojenia jest równa 4.2 K

współczynnik bezpieczeństwa - α_b=0.75

prąd roboczy - I_r=200A

współczynnik miedzi do nadprzewodnika C_SC=1.5

współczynnik zapełnienia uzwojenia - λ=0.20

gęstość prądu J_c dla nadprzewodnika NbTi wynosi 0.375⋅10⁹ A/m²

gęstość prądu J_c dla nadprzewodnika Nb₃Sn wynosi 4.3⋅10⁹ A/m²

3. Przekrój cewki nadprzewodnikowej.

4. Projektowanie geometryczne uzwojeń przy zastosowaniu współczynnika Fabry'ego i minimalizacji objętości.

Przeprowadzone obliczenia projektu cewek i elektromagnesu są obarczone błędem wynikającym z nieuwzględnienia wartości indukcji na początku nawinięcia cewki.

1.wykres zależności B w funkcji promienia nawinięcia cewki

Z przedstawionej zależności wynika że indukcja na krawędzi wewnętrznej cewki ma większą wartość niż w środku. Tak więc , aby nadprzewodnik nie wyszedł ze stanu nadprewodnictwa (przekroczenie prądu krytycznego dla tej wartości indukcji) należało by uwzględnić nowe warunki do obliczeń parametrów cewek.

(np. pomniejszyć współczynnik α_b) .

Wartość indukcji na wewnętrznej krawędzi cewki została obliczona za pomocą programu

B₀=8.5 T B(a₁)≈ T

4.1. Projekt cewki z nadprzewodnika NbTi.

Wartość indukcji magnetycznej w środku solenoidu -B₀ : B₀=μ₀⋅λ⋅J_r⋅a₁⋅F(α;β)

gdzie F(α;β)-współczynnik Fabry'ego wyrażony równaniem:

Objętość uzwojenia określa równanie: V(α;β)=2⋅Π⋅a₁³⋅v(α;β)

gdzie v(α;β)=β(α²-1)

Wartości α, β, F(α;β) oraz minimalną wartość V(α;β) obliczono za pomocą komputera dla:

J_r=J_c⋅α_b=0.375⋅10⁹ A/m² ⋅ 0.75=0.28125⋅10⁹ A/m²

μ₀=4⋅Π⋅10^-7 H/m.

B₀=8.5 T

a₁=0.15 m

Wyniki:

F(α;β)=0.801669343

α=2.0345823224

β=1.1688000003

V_min=0.07781401522 m³

Promień zewnętrzny cewki a₂=α⋅a₁=0.30519 m

Długość cewki 2⋅b=2⋅β⋅a₁=0.35064 m

Pole przekroju nadprzewodnika w przewodzie:

A_SC=

Pole przekroju miedzi w przewodzie A_cu=A_SC⋅C_SC=7.111⋅10^-7 m² ⋅1.5=1.0666⋅10^-6 m²

Pole przekroju przewodu A_p=A_cu+A_SC=1.0666⋅10^-6 m²+7.1111⋅10^-7 m²=1.7777⋅10^-6 m²

Średnica przewodu f_przew=2⋅0.0015045 m

Pole przekroju cewki A=2⋅b(a₂-a₁)= 0,054416

Liczba zwojów w cewce N_zw= 15305 zw

Długość przewodu l_przew=N_zw⋅Π⋅(a₁+a₂)= 21885,8 m

Indukcyjność własna cewki L==59.34 H

Energia zgromadzona w polu magnetycznym cewki

E=1.187 MJ

Pole przekroju włókna A_w=

Liczba włókien w przewodzie N_w=

4.2. Rozkład pola magnetycznego.

B(ξ)=μ₀⋅λ⋅J_r⋅a₁⋅F(ξ)

gdzie F(ξ) - zmodyfikowany współczynnik Fabry'ego

F(ξ)=

gdzie ξ= - odległość względna od środka cewki mierzona na osi cewki

Dla końca cewki z=b ⇒ ξ=β

F(ξ)=0.4335901606

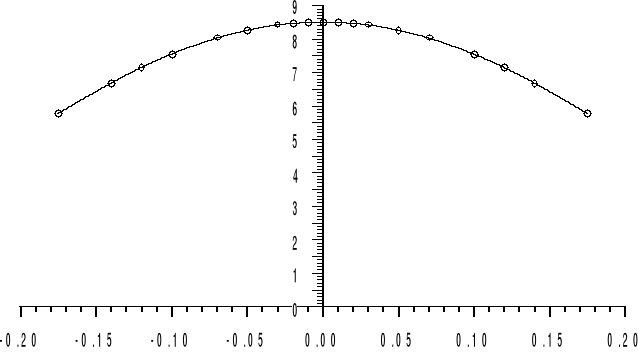
B(ξ)=5.7771405562 T

Wartości indukcji magnetycznej zestawione są na charakterystyce

Współczynnik niejednorodności pola magnetycznego na osi cewki

Parametry cewki

Promień wewnętrzny a1	0.15 m
Promień zewnętrzny a2	0.305 m
Długość cewki 2b	0.3506 m.
Prąd roboczy Ir	200 A
Liczba zwojów w cewce Nzw	15305
Indukcja magnetyczna w środku cewki B0	8.5 T
Maksymalna indukcja magnetyczna	8.5 T
Współczynnik niejednorodności pola Δξ	0.3203
Indukcyjność własna cewki L	59.34 H
Energia cewki E	1.187 MJ

Parametry przewodu

Typ przewodu	T 9055-1.5/1.5 TV
Nadprzewodnik	NbTi
Średnica przewodu fprzew	0.001504 m
Średnica włókna φw	10 10^-6 m
Liczba włókien	9055
Współczynnik CSC	1.5
Długość przewodu lprzew	21885.8 m

Charakterystyka indukcji magnetycznej na osi cewki:

B [T]

l [m]

4.3. Projekt cewki z nadprzewodnika Nb₃Sn.

Wartość indukcji magnetycznej w środku solenoidu : B₀=μ₀⋅λ⋅J_r⋅a₁⋅F(α;β)

gdzie F(α;β)-współczynnik Fabry'ego wyrażony równaniem:

Objętość uzwojenia określa równanie: V(α;β)=2⋅Π⋅a₁³⋅v(α;β)

gdzie v(α;β)=β(α²-1)

Wartości α, β, F(α;β) oraz minimalną wartość V(α;β) obliczono za pomocą komputera dla:

J_r=J_c⋅α_b=4.3⋅10⁹ A/m² ⋅ 0.75=3.225⋅10⁹ A/m²

μ₀=4⋅Π⋅10^-7 H/m.

B₀=8.5 T

a₁=0.15 m.

Wyniki obliczeń F(α;β)=0.069913024

α=1.1574729962

β=0.4068000003

V_min=0.0029307991 m³

Promień zewnętrzny cewki a₂=α⋅a₁=0.173621 m

Długość cewki 2⋅b=2⋅β⋅a₁=0.12204 m

Pole przekroju nadprzewodnika w przewodzie: A_SC=6.20155⋅10^-8 m²

Pole przekroju miedzi w przewodzie A_cu=A_SC⋅C_SC=9.3023⋅10^-8 m²

Pole przekroju przewodu A_p=A_cu+A_SC=1.55039⋅10^-7 m²

Średnica przewodu f_przew=2⋅0.0004443 m

Pole przekroju cewki A=2⋅b(a₂-a₁)=0.002883 m²

Liczba zwojów w cewce N_zw=9297 zw

Długość przewodu l_przew=N_zw⋅Π⋅(a₁+a₂)=9451.9 m

Indukcyjność własna cewki L=62.91 H

Energia zgromadzona w polu magnetycznym cewki E=1.26 MJ

Pole przekroju włókna A_w=

Liczba włókien w przewodzie N_w=

Rozkład pola magnetycznego.

B(ξ)=μ₀⋅λ⋅J_r⋅a₁⋅F(ξ)

H(ξ)=B(ξ)/μ₀

Wartości pola magnetycznego zestawione są na charakterystyce

gdzie F(ξ) - zmodyfikowany współczynnik Fabry'ego

F(ξ)=

gdzie ξ= - odległość względna od środka cewki mierzona na osi cewki

Dla końca cewki z=b ⇒ ξ=β

F(ξ)=0.04743583785

B(ξ)=7.2473090981 T

H(ξ)=56,5 MA/m.

Wartości indukcji magnetycznej zestawione są na charakterystyce

Współczynnik niejednorodności pola magnetycznego na osi cewki

Parametry cewki

Promień wewnętrzny a1	0.15 m
Promień zewnętrzny a2	0.1736 m
Długość cewki 2b	0.122 m
Prąd roboczy Ir	200 A
Liczba zwojów w cewce Nzw	9297
Indukcja magnetyczna w środku cewki B0	8.5 T
Maksymalna indukcja magnetyczna	8.5 T
Współczynnik niejednorodności pola Δξ	0.1474
Indukcyjność własna cewki L	62.91 H
Energia cewki E	1.26 MJ

Parametry przewodu

Typ przewodu	T 790-1.5/0.4 TV
Nadprzewodnik	Nb3Sn
Średnica przewodu fprzew	0.000444 m
Średnica włókna φw	10 10^-6 m
Liczba włókien	790
Współczynnik CSC	1.5
Długość przewodu lprzew	9451.9 m.

Charakterystyka pola magnetycznego na osi cewki:

H [A/m ⋅10⁷]

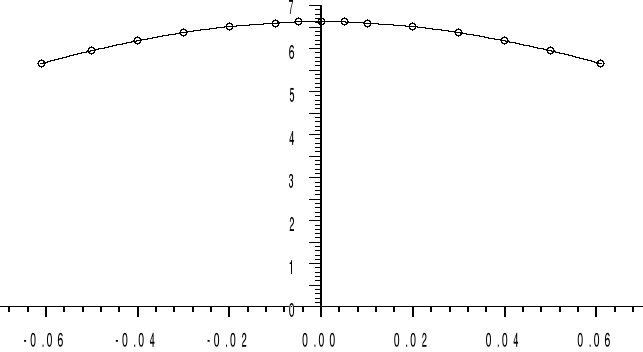
l [m]

Projekt elektromagnesu dwusekcyjnego z NbTi i Nb₃Sn.

Sekcja pierwsza z Nb₃Sn.

Założenia:

- Szerokość nawinięcia sekcji 1 wynosi połowę cewki Nb₃Sn

- a₁ =0.15 m

- a₁₂ =(a₂+a₁)/2=0.16181 m

- β=0.4068

- α=a₁₂/a₁=1.07873

- J_r=J_c⋅α_b=4.3⋅10⁹ A/m² ⋅ 0.75=3.225⋅10⁹ A/m²

- μ₀=4⋅Π⋅10^-7 H/m

Wartość indukcji magnetycznej w środku sekcji pierwszej B₀=μ₀⋅λ⋅J_r⋅a₁⋅F(α;β)

gdzie F(α;β)-współczynnik Fabry'ego wyrażony równaniem:

Objętość uzwojenia określa równanie: V₁(α;β)=2⋅Π⋅a₁³⋅v(α;β)

gdzie v(α;β)=β(α²-1)

na osi elektromagnesu.

Wartości F(α;β), B₀ oraz minimalną wartość V₁(α;β) obliczono za pomocą komputera i wynoszą:

F(α;β)=0.0360724

B₀=4.3857 T

V₁=0.0014118 m³

Długość sekcji 1 2⋅b=2⋅β⋅a₁=0.12204 m

Pole przekroju nadprzewodnika w przewodzie: A_SC=6.20155⋅10^-8 m²

Pole przekroju miedzi w przewodzie A_cu=A_SC⋅C_SC=9.3023⋅10^-8 m²

Pole przekroju przewodu A_p=A_cu+A_SC=1.55039⋅10^-7 m²

Średnica przewodu f_przew=2⋅0.0004443 m

Pole przekroju sekcji 1 A=2⋅b(a₁₂-a₁)=0.0014413 m²

Liczba zwojów w sekcji 1 N_zw= 4649zw

Długość przewodu sekcji 1 l_przew=N_zw⋅Π⋅(a₁₂+a₂)=4553 m

Indukcyjność własna sekcji 1 L=5.006 H

Energia zgromadzona w polu magnet. sekcji 1 E=0.1 MJ

Pole przekroju włókna A_w=

Liczba włókien w przewodzie N_w=

4.5.2. Rozkład pola magnetycznego sekcji 1.

B(ξ)=μ₀⋅λ⋅J_r⋅a₁⋅F(ξ)

H(ξ)=B(ξ)/μ₀

Wartości pola magnetycznego zestawione są na charakterystyce

Współczynnik niejednorodności pola magnetycznego na osi cewki

4.5.3. Sekcja druga z NbTi.

Założenia:

- Cewka NbTi nawinięta na sekcji pierwszej.

- a₁ =0.16181 m

- β=b/a₁= 0.06102/0.16181=0.3771

- B₂=B₀-B₁= 8.5 - 4.3857 =4.1143 T

- dla B₂ z tabeli odczytujemy J_c=1.37142⋅10⁹ A/m²

- μ₀=4⋅Π⋅10^-7 H/m.

F(α;β)-współczynnik Fabry'ego F(α;β)=B_o/μ₀⋅λ⋅J_r⋅a₁₌0,09836088

dla α=1.2452

Objętość uzwojenia : V₂(α;β)=2⋅Π⋅a₁³⋅v(α;β) =0.05526 m²

Długość sekcji 2 2⋅b=2⋅β⋅a₁=0.12204 m

Promień zewn. a₂=0.2015 m

Pole przekroju nadprzewodnika w przewodzie: A_SC=6.20155⋅10^-8 m²

Pole przekroju miedzi w przewodzie A_cu=A_SC⋅C_SC=9.3023⋅10^-8 m²

Pole przekroju przewodu A_p=A_cu+A_SC=1.55039⋅10^-7 m²

Średnica przewodu f_przew=2⋅0.0004443 m

Pole przekroju sekcji 2 A=2⋅b(a₂-a₁)= 0.0016054 m²

Liczba zwojów w sekcji 2 N_zw=15616 zw

Długość przewodu sekcji 2 l_przew=N_zw⋅Π⋅(a₁+a₂)= 17823 m

Indukcyjność własna sekcji 2 L=206,5 H

Energia zgromadzona w polu magnet. sekcji 2 E=4,13 MJ

Pole przekroju włókna A_w=

Liczba włókien w przewodzie N_w=

Rozkład pola magnetycznego sekcji 2.

B(ξ)=μ₀⋅λ⋅J_r⋅a₁⋅F(ξ)

H(ξ)=B(ξ)/μ₀

Wartości pola magnetycznego zestawione są na charakterystyce

Współczynnik niejednorodności pola magnetycznego na osi cewki

Parametry sekcji

	Sekcja 1	Sekcja 2
Promień wewnętrzny a1	0.15 m.	0.1618 m.
Promień zewnętrzny a2	0.1618 m	0.2015 m.
Długość cewki 2b	0.122 m.	0.122 m.
Prąd roboczy Ir	200 A	200 A
Liczba zwojów w cewce Nzw	4649	15616
Indukcja magnetyczna w środku cewki B0	8.5 T	8.5 T
Maksymalna indukcja magnetyczna	4.385 T	4.114 T
Współczynnik niejednorodności pola Δξ	0.154	0.144
Indukcyjność własna cewki L	5.006 H	206,5 H
Energia cewki E	0.1 MJ	4,13 MJ

Parametry przewodów

Typ przewodu	T 790-1.5/0.4 TV	T 9055-1.5/1.5 TV
Nadprzewodnik	Nb3Sn	NbTi
Średnica przewodu fprzew	0.000444 m	0.001504 m
Średnica włókna φw	10 10^-6 m	10 10^-6 m.
Liczba włókien	790	9055
Współczynnik CSC	1.5	1.5
Długość przewodu lprzew	4553 m	17823 m.

Charakterystyka pola magnetycznego elektromagnesu.

H [A/m.]

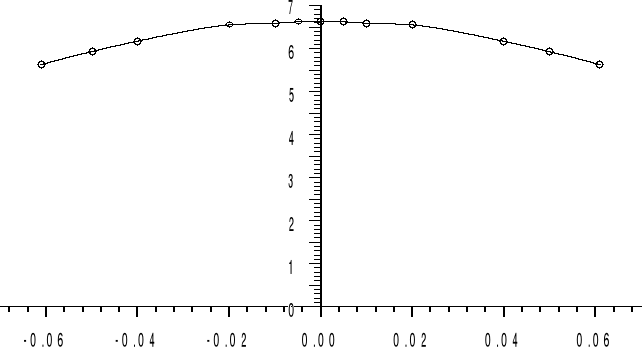
l [m.]

5. Wnioski.

Projektowanie geometryczne uzwojeń przeprowadzone zostało za pomocą napisanego programu komputerowego w Turbo Pascalu .

Brak danych na temat cennika nadprzewodników nie pozwolił na pełną minimalizację kosztorystyczną i geometryczną elektromagnesu nadprzewodnikowego dwusekcyjnego.

Minimalizację elektromagnesu nadprzewodnikowego dokonano na zasadzie nawinięcia sekcji z NbTi na sekcji Nb₃Sn.

Rozkład pola elektromagnesu jest sumą wartości pola magnetycznego sekcji 1 i sekcji 2.

Wykonane obliczenia mogą zostać wykorzystane do zaprojektowania całego kriomagnesu ( obliczenia karkasu ,wymiarów kriostatu ,układu zasilania i zabezpieczenia, zapotrzebowania helu i przepustowości prądowych).

---