1000299f2992727065769B7890992 n

—    wartość oczekiwanej stopy zwrotu powinna w czasie prognozy zmieniać się w wyniku zmian stopy inflacji, ryzyka systematycznego lub też struktury' kapitałowej.

Firmy funkcjonujące w gospodarce rynkowej, podejmując decyzje rozwojowe, muszą się kierować wskazaniami rynku finansowego. Rynek ten pośrednio wyznacza koszt poszczególnych źródeł kapitału na finansowanie projektów inwestycyjnych.

Przedsiębiorstwa finansują projekty inwestycyjne korzystając ze źródeł zewnętrznych, w formie kapitału obcego, np. kredytu bankowego, emisji obligacji, i kapitału własnego, np. emisji akcji, oraz wewnętrznych, np. z zysków zatrzymanych¹.

W praktyce — jak wskazują ekonomiści — występują cztery podstawowe źródła finansowania długoterminowego, a mianowicie (Altmar. 19S6, s. 126, za Jerzemowską 1996, s. 39):

—    zadłużenie długoterminowe;

—    akcje uprzywilejowane;

—    zyski zatrzymane;

—    akrje zwykłe.

Kolejno zostaną omówione czynności związane z wyznaczaniem kosztu kapitału, pochodzącego z wyodrębnionych wyżej źródeł finansowania dhigookreso-

Koszt kapitału obcego

Koszt kapitału z emisji obligacji. W krajach o rozwiniętej gospodarce rynkowej zaciąganie długu odbywa się głównie przez emisję obligacji jako średnio-i długoterminowych papierów dłużnych, rzadziej zaś przez zaciąganie kredytu bankowego (Dułiniec 1998, s 70). Koszt kapitału z tytułu sprzedaży papierów dłużnych zależy od ich rentowności, która określona jest wysokością nominalnego oprocentowania obligaqi oraz różnicą pomiędzy ceną nabycia i odsprzedaży przez inwestora na rynku kapitałowym oraz terminem wykupu.

Do wyceny kosztu kapitału obligacji przedsiębiorstw pomocny jest ogólny model wyceny wartości rynkowej obligacji, który możemy zapisać:

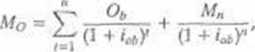
gdzie:

Mu — rynkowa wartość obligacji,

O_b — odsetki od obligacji,

M„ — cena wykupu obligacji, iu, — stopa zwrotu z obligacji

Z modelu wynika, że stopa rentowności obligacji /<*,, będąca dalej podstawą wyceny kosztu kapitału z obligacji, jest to stopa dyskontowa, dla której wartość zdyskontowana przyszłych wpływów inwestora z tytułu posiadanych obligacji równa się cenie nabycia tych obligacji. Stąd wniosek, że jeżeli obligacje >ą sprzedawane według wartości nominalnej Af„, to rentowność obligacji jest równa nominalnej stopie oprocentowania tychże obligacji. Z kolei przy sprzedaży z dyskontem rentowność obligacji jest wyższa od oprocentowania nominalnego, a przy sprzedaży z premią zależność jest odwrotna

Znajomość poziomu rentowności obligacji jest niezbędna do oszacowania kosztu kapitału obcego w przedsiębiorstwie emitującym papiery dłużne. Faktycznie koszt długu (ij) jest mniejszy od stopy zwrotu (r_rv>) z powodu korzyści wynikających z taktu, ze oprocentowanie długu jest kosztem zmniejszającym podstawę opodatkowania. Zatem

i_rf = UO s).

gdzie:

ij — koszt długu z emisji obligacji (uwzględniający opodatkowanie), j — sławka podatku dochodowego.

0    wysokości kosztu kapitału z obligacji stanowią również koszty emisji obligacji (przygotowanie projektu emisyjnego lub memorandum informacyjnego, honoraria doradców, audytorów, prowizje dla gwaranta czy organizatora emisji itp.).

Generalnie koszt kapitału z emisji obligacji zależy od stopy procentowej

1    częstotliwości wypłaty oprocentowania, czasu do wykupu, ceny emisyjnej skorygowanej o koszty emisji oraz oszczędności podatkowych. Uwzględniając przyjętą symbolikę, możemy wyznaczyć koszt kapitału z nowej emisji obligacji, za pomocą formuły zdyskontowanych przepływów gotówki:

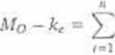
Offl - -o

(1 + W

+

Mn

(1+i.tr'

gdzie:

k, — koszt emisji obligacji.

Formula ta oznacza, że koszt kapitału /. emisji obligacji określa stopa procentowa, przy której zdyskontowana wartość wydatków związanych z płatnością odsetek i wykupem obligacji zrównoważy wartość wpływów uzyskanych z obligacji po uwzględnieniu kosztów emisji. Emitent, aby sprzedać obligacje, musi zapewnić inwestorom w obligacje odpowiednio atrakcyjny poziom stopy zw rotu w porównaniu do innych możliwości lokowania kapitału w danych warunkach rynku finansowego.

Koszt kapitału pochodzącego z emisji obligacji można wyliczyć stosując również prostą formule statyczna:

ii ^a p(* -*)•

gdzie

p — stopa oprocentowania obliracji

1

Proaicm /marnowania inwe»fyq. j*łt •.——l.'? c~jw;ar.y w literaturze przedmiotu i w związku z I) m nie zutta: opuany w te; pr«c\

' 2 uwagi na obszerną literaturę na temat wyceny kosztu kapitału, przedstawiono 5prawy podstaw owe, i»totne w niniejszym opracowaniu.