17252 Untitled Scanned 27 (8)

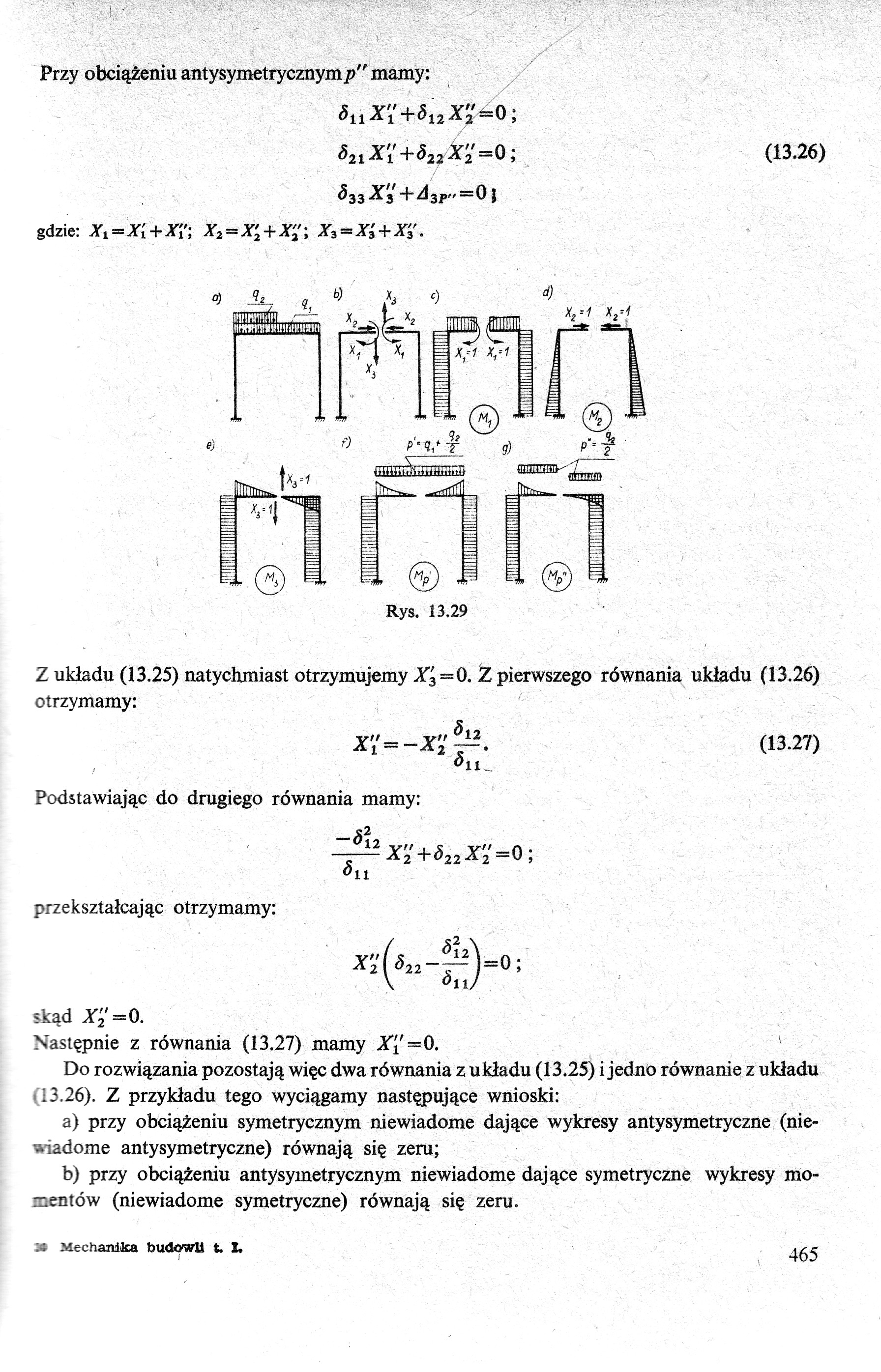
Przy obciążeniu antysymetrycznymp" mamy:

b_xxX'l+b^X'iM\

^21^1+^22^2=0;    (13.26)

^33 X'Ś +^3P" = 0 }

gdzie: X₁_ = X[ + X'_l’\ X₂=X'₂ + X'₂'‘, X₃ = Xi + X'₃'.

Z układu (13.25) natychmiast otrzymujemy X'₃=0. Z pierwszego równania układu (13.26) otrzymamy:

X” = -X’±    (13.27)

Podstawiając do drugiego równania mamy:

~Sl ₂

—^^'+022^2=0;

£>11

przekształcając otrzymamy: skąd Zj'=0.

Następnie z równania (13.27) mamy Xj'=0.

Do rozwiązania pozostają więc dwa równania z układu (13.25) i jedno równanie z układu i 13.26). Z przykładu tego wyciągamy następujące wnioski:

a)    przy obciążeniu symetrycznym niewiadome dające wykresy antysymetryczne (niewiadome antysymetryczne) równają się zeru;

b)    przy obciążeniu antysymetrycznym niewiadome dające symetryczne wykresy momentów (niewiadome symetryczne) równają się zeru.

465

3» Mechanika budowli t I.