17780 Untitled Scanned 27

- 54 -

zmianie wartości sygnału x_i# zmiany wartości sygnałów bx_i i cXj winny dokonywać się jednocześnie, co praktycznie nie jest możliwe. Ha skutek niejednoczesności tych zmian pojawia się chwilowo stan, w którym sygnały reprezentujące wyrażenia bx_i i cXj_L jednocześnie przejmują wartości 0, co Jest przyczyną nieciągłości stanu sygnału wyjściowego.

Omawiany przypadek wystąpi wtedy, kiedy przy ustalaniu postaci normalnej w tablicy Kamaugha pozostaną nie sklejone sąsiednie jedynki, np. w układzie (rys.2.21) zrealizowanym na podstawie równania

y «= x₁ *x₂ +    **2

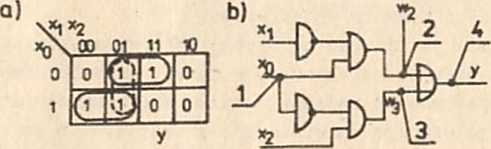
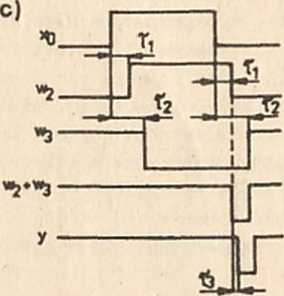
Rys.2.21. Hazard statyczny: a) tablica Kar-naugha; b) schemat układu z hazardem; c) przebiegi sygnałów w wybranych punktach układu

Hazard statyczny wystąpi 1;u przy zmianach sygnału x^ gdy i . Proces powstawania hazardu wyjaśnia rys.2.21c. Przebiegi sygnałów w punktach 1,2, 3, 4 układu (rys.2.21b), oznaczone odpowiednio przez: x₁, w₂# w-j i y# wykreślono przy założeniu, że czas opóźnienia r- między punktami 1 i 2 jest mniejszy od czasu opóźnienia Tg między punktami 1 i 3.

Przyczyna powstawania hazardu statycznego znika, jeżeli zrealizuje się układ z uwzględnieniem przekształcenia

y o a + b*x₁ + c«5E_i = a + b»x^ + c«x^ + b*c

które odpowiada dodatkowemu sklejeniu w tablicy Karnaugha (linia przerywana na rys.2.21a).

Analogicznie, jeżeli funkcja, którą realizuje układ ma postać

y = d • (e + x^)»(t + 5ć_i)

\

gdzie: x₁ - jeden z argumentów funkcji, d - iloczyn elementarnych sum, e, f - elementarne sumy, to w układzie wystąpi hazard w zerach podczas zmian sygnału x^ gdy d=1, e=0, f=0. Powyższą postać uzyskuje się jeżeli w tablicy Karnaugha pozostaną nie sklejone sąsiednie zera.

Usuwanie hazardu w zerach polega na rozbudowie układu przy wykorzystaniu przekształcenia

y = d«(e + x_i)-(f + 5E_ł ) = d-fe + x_±)‘(f + ać^fe + f)

któremu odpowiada dodatkowe sklejenie sąsiednich zer w tablicy Karnaugha.

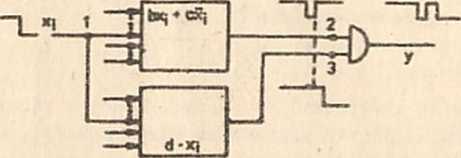
Rys.2.22. Układ z hazardem dynamicznym

Przyczyną wystąpienia w układzie hazardu dynamicznego jert hazard statyczny w jednej z gałęzi układu - rys.2.22. foteli w stanie gdy b=1, c»1, d=1 podczas zmiany sygnału x^, np, z 1 na 0, w gałęzi między punktami 1 i 2 wystąpi hazard statyczny, a czas opóźnienia między punktami 1 i 2 jest mniejszy niż czas opóźnienia między punktami 1 i 3, to chwilowy zanik sygnału

W DUnkf.lA 9. onoWnH^nnu V,ntr.~-------- ,---—---i