19301 IMG�80 (2)

żającą miarę wypadkową niepewności wyniku pomiaru w postaci wypadkowego odchylenia standardowego Gdybyśmy potrzebowali przejść do przedziałowej miary niepewności, skorzystalibyśmy z formuły (1.9a).

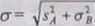
(1.17)

1.6.6. Przenoszenie błędów i przenoszenie niepewności

Mówiliśmy już, że do oceny błędu wyniku pomiaru lub do oceny niepewności dochodzimy analizując z osobna czynniki, zjawiska, charakteryzowane za pomocą właściwych im wielkości fizycznych, które składają się na podstawowy układ warunków doświadczenia pomiarowego i oceniając, jak błąd lub nieokreśloność danego czynnika może wpływać na błąd lub nieokreśloność wyniku pomiaru. W ten sposób dochodzimy do wyznaczenia (oszacowania) odpowiednio bądź błędu, bądź niepewności, wynikających z działania każdego czynnika. Nazwaliśmy otrzymane wyniki analizy składowymi błędu lub składowymi niepewności. Składowe błędu można złożyć (suma algebraiczna błędu) i usunąć uwzględniając odpowiednią poprawkę, z czego pozostanie niepewność wynikająca z niedoskonałego poprawiania, bo poprawka nie może mieć absolutnej dokładności. Ale pozostanie też niepewność z powodu każdego błędu, którego nie usunęliśmy i te niepewności jako cząstkowe udziały wejdą do niepewności typu B.

Ocenę niepewności końcowego wyniku pomiaru osiągamy w działaniu trzystopniowym. dochodzimy najpierw do danych cząstkowych niepewności typu B, następnie składamy te dane cząstkowe (1.16), żeby otrzymać niepewność typu B i dopiero w trzecim kroku wyznaczamy wypadkową niepewność składając A i B (1.17). Rachunki analizy błędów oraz niepewności możemy wykonywać w ten sposób tylko wówczas, co zastrzegliśmy w poprzednim paragrafie, gdy na każdym poziomie działań nasze cząstkowe składowe błędu lub cząstkowe niepewności wyrażone są jako błąd lub niepewność wyniku końcowego, a więc są wyrażone za pomocą tej samej jednostki (co wynik pomiaru). Gdy jednak pierwotnie mamy dane o błędach lub niepewnościach charakteryzujących nieokreśloność różnych wielkości podstawowego układu warunków doświadczenia pomiarowego, to powstaje problem, jak obliczyć ich wpływ na nieokreśloność wyniku pomiaru i jak je następnie złożyć. Ten problem w miernictwie nazywa się przenoszeniem błędów i niepewności (w domyśle: z jednej wielkości na inną wielkość, gdy one związane są jakąś funkcją)

Układ warunków - powtarzamy - widzimy jako pewną funkcję (1 1), w której każdy fizyczny warunek (czynnik) przedstawiony jest za pomocą zmiennych niezależnych x_h reprezentujących charakterystyczne dla układu warunków wielkości, a wpływ każdego z nich na wynik pomiaru y realizuje się poprzez funkcję fi jest więc zależny od tej funkcji. Z funkcji f wynika wrażliwość y na ewentualne zmiany (nieokreśloność) danego czynnika (danej zmiennej) Matematycznie wrażliwość ze względu na daną zmienną wyraża się wartością pochodnej danej funkcji względem tej zmiennej, w naszym przypadku pochodnej cząstkowej, bo mamy funkcję wielu zmiennych Im większa jest wartość pochodnej (bezwzględna wartość!) względem danej wielkości, tym większa jest - jak mówimy - wrażliwość wyniku pomiaru na niepewność (nieokreśloność) danej wielkości albo na błąd danej wielkości.

Funkcję (1.1) - jak wiemy - możemy odczytać na dwa sposoby. W sposób ogólny -jako definiującą wskazanie przyrządu y będące funkcją wielkości x,_t wielkości określających układ warunków doświadczenia pomiarowego. Wówczas X; lub ewentualnie kilka do x, są wielkościami wejściowymi przyrządu i wg równania przetwarzania przyrządu powodują wskazanie j<, a pozostałe określają podstawowy układ warunków doświadczenia Może być też tak - jak wiemy, że każda z wielkości do x, jest bezpośrednio mierzona osobnymi przyrządami z jakąś znaną niepewnością, a my na podstawie znanej funkcji /1 wartości z, będziemy wyznaczać y. W każdym przypadku powstaje zadanie: jak przenoszą się błędy lub niepewności (nieokreśloność) wartości x, na wynik y?

Przykład. Rczystywność materiału przewodzącego prąd elektryczny wyznacza się z wymiarów próbki lego materiału i z pomiaru rezystancji lej próbki, a więc pośrednio Rezystancję leź możemy wyznaczyć pośrednio z prawa Ohma mierząc spadek napięcia na próbce, gdy przez próbkę przepływa mierzony prąd Mamy tu do czynienia z tzw. pomiarem pośrednim, o którym była juZ mowa Równocześnie wiadomo. Ze rczystywność będzie załeZala od temperatury, fizycznego i chemicznego stanu próbki danego materiału Te ostatnie czynniki składać się będą na układ warunków wyniku pomiaru.

Zauważmy, Ze w ogólnym przypadku, rczystywności nie potrafimy inaczej zmierzyć, jak tylko pośrednio (chyba Ze zbudowalibyśmy skomplikowaną „machinę" do pomiaru rezystywności). Natomiast np moc elektryczną można mierzyć jednym przyrządem (watomierzem) albo - raczej w szczególnych okolicznościach - kilkoma przyrządami (np. woltomierzem, amperomierzem, fazomierzem).

Najprostszy sposób rozwiązania takiego zagadnienia oparty jest na rachunku różniczkowym, jest przybliżony, ale wystarczająco dokładny do wyznaczania błędu wypadkowego (lub niepewności wypadkowej). Przybliżenie polega na tym, że dowolną fbnkęję f linearyzujemy, a więc aproksymujemy płaszczyzną styczną do powierzchni, która geometrycznie przedstawiałaby naszą funkcję/, płaszczyzną styczną w punkcie o współrzędnych wyznaczonych przez wartości x,. Skutek uproszczenia zależeć będzie od tego, jak daleko będziemy oddalać się od punktu styczności, czyli zależeć będzie od wartości występujących błędów (lub niepewności). W dziedzinie pomiarów elektrycznych rachunki w ten sposób wykonane są wystarczająco dokładne dla analizy dokładności, bo błędy z zasady są bardzo małe.

Korzystamy też z linearyzacji (czyli z rachunku różniczkowego) przy obliczaniu wypadkowej niepewności a_y (lub s,) zmiennej y na podstawie danych a, zmiennych (losowych) x, i funkcji / ale w tym zastosowaniu linearyzacja prowadzi do dodatkowego źródła błędu, bo wariancja jest funkcją nieliniową (dokładnie kwadratową), lecz ten fakt też ignoruje się w metrologii Ponadto ograniczamy się do przypadku zmiennych losowych niezależnych (nieskorelowanych).

Błędy cząstkowe Ą, zawarte w y, a wywołane błędami A_a wielkości x,, określa zależność (1.18), natomiast złożenie ich wg (1.19) wyznaczy błąd wypadkowy A, wartości y. W tym rachunku przyjęliśmy niezależność zmian każdej zmiennej. Wartość pochodnej y względem x, jest tu wartością współczynnika wrażliwości y na daną wielkość x, Otrzymaną wartość A, możemy przeliczyć na poprawkę wg (1.5) ■ ją uwzględnić.

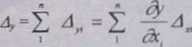
(1.18)

(1.19)

Wartość niepewności cząstkowej Op (wyrażonej za pomocą odchylenia standardowego) otrzymamy z takiej samej zależności co błąd cząstkowy (1.18), z tym Ze zamiast Aa wstawimy odpowiednio <r„ Natomiast niepewność wypadkowa a, wyrazi się analogicznie do (1.16) zależnością (1.20). Na każdy składnik występujący pod pierwiastkiem

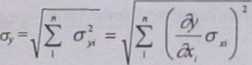
(120)

45